Question

1．圆O中，弦AB满足|AB|=2，则$\overrightarrow{AB}$•$\overrightarrow{AO}$=（　　）

• A． 2
• B． 1
• C． $\frac{1}{2}$
• D． 4

Answer 1

分析 由圆的弦心距垂直平分弦长，将$\overrightarrow{AO}$用$\overrightarrow{AC}+\overrightarrow{CO}$表示，展开后整理得答案．

解答 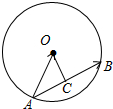解：如图，取AB的中点C，则OC⊥AB且AB=2AC，
$\overrightarrow{AB}$•$\overrightarrow{AO}$=$\overrightarrow{AO}•2\overrightarrow{AC}$=2$\overrightarrow{AO}•\overrightarrow{AC}$
=2（$\overrightarrow{AC}+\overrightarrow{CO}$）•$\overrightarrow{AC}$=$2|\overrightarrow{AC}{|}^{2}+2\overrightarrow{CO}•\overrightarrow{AC}$=2$|\overrightarrow{AC}{|}^{2}=2$．
故选：A．

点评 本题考查平面向量的数量积运算，考查圆与平面几何知识，向量垂直的条件等，是中档题．