
分析 (1)由递推公式能求出a2t和a3.
(2)先求出a2n+1-a2n-1=4n+(-2)n-1,利用累加法求出a2n+1,由a2n=a2n+1-4n得到a2n,由此能求出{an}的通项公式.
(3)由a2n=$\frac{{4}^{n}}{3}$-$\frac{(-2)^{n}}{3}$,得bn=4n-(-2)n,从而$\frac{1}{{b}_{n}}$=$\frac{1}{{4}^{n}-(-2)^{n}}$,由此能证明$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$<$\frac{7}{12}$.
解答 解:(1)∵数列{an}中,a1=1,a2n=a2n-1+(-2)n-1,a2n+1=a2n+4n,n∈N*,
∴a2=a1+(-2)0=1+1=2,
a3=a2+4=2+4=6.
(2)∵a2n=a2n-1+(-2)n-1,a2n+1=a2n+4n,n∈N*
∴a2n+1-a2n=4n,${a}_{2n}-{a}_{2n-1}=(-2)^{n-1}$,
∴a2n+1-a2n-1=4n+(-2)n-1,
∴a2n+1=a1+a3-a1+a5-a3+…+a2n+1-a2n-1
=1+(4+42+…+4n)+[(-2)0+(-2)+…+(-2)n-1]
=1+$\frac{4(1-{4}^{n})}{1-4}$+$\frac{1-(-2)^{n}}{1+2}$
=$\frac{{4}^{n+1}}{3}$-$\frac{(-2)^{n}}{3}$.
∴a2n=a2n+1-4n=$\frac{{4}^{n+1}}{3}$-$\frac{(-2)^{n}}{3}$-4n=$\frac{{4}^{n}}{3}$-$\frac{(-2)^{n}}{3}$.
∴{an}的通项公式:${a}_{n}=\left\{\begin{array}{l}{\frac{{4}^{\frac{n+1}{2}-(-2)^{\frac{n-1}{2}}}}{3},n为奇数}\\{\frac{{4}^{\frac{n}{2}-(-2)^{\frac{n}{2}}}}{3},n为偶数}\end{array}\right.$.
(3)∵a2n=$\frac{{4}^{n}}{3}$-$\frac{(-2)^{n}}{3}$,bn=a2n+2-a2n,
∴bn=$\frac{{4}^{n+1}}{3}-\frac{(-2)^{n+1}}{3}$-$\frac{{4}^{n}}{3}$+$\frac{(-2)^{n}}{3}$=4n-(-2)n,∴$\frac{1}{{b}_{n}}$=$\frac{1}{{4}^{n}-(-2)^{n}}$,
当n为奇数时,$\frac{1}{{b}_{n}}$=$\frac{1}{{4}^{n}+{2}^{n}}$=$\frac{1}{{2}^{n}({2}^{n}+1)}$=$\frac{1}{{2}^{n}}$-$\frac{1}{{2}^{n}+1}$,
当n为偶数时,$\frac{1}{{b}_{n}}$=$\frac{1}{{4}^{n}-{2}^{n}}$=$\frac{1}{{2}^{n}({2}^{n}-1)}$=$\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n}}$,
∴当n为奇数时,$\frac{1}{{2}^{n}}-\frac{1}{{2}^{n-1}}$<0,
$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$
=$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+$\frac{1}{8}-\frac{1}{9}$+$\frac{1}{15}-\frac{1}{16}$+…+$\frac{1}{{2}^{n-1}-1}-\frac{1}{{2}^{n-1}}$+$\frac{1}{{2}^{n}}-\frac{1}{{2}^{n}+1}$
<$\frac{1}{2}-\frac{1}{{2}^{n}+1}$<$\frac{1}{2}$.
当n为偶数时,$\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n-1}+1}$<0
$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$
=$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+$\frac{1}{8}-\frac{1}{9}$+$\frac{1}{15}-\frac{1}{16}$+…+$\frac{1}{{2}^{n-1}}-\frac{1}{{2}^{n-1}+1}$+$\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n}}$
<$\frac{1}{2}-\frac{1}{{2}^{n}}$<$\frac{1}{2}$.
综上,$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$<$\frac{7}{12}$.
点评 本题考查数列的通项公式的求法,考查数列前n项和小于$\frac{7}{12}$的证明,综合性强,难度大,解题时要注意裂项求和法和分类讨论思想的合理运用.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:解答题
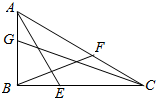 如图,△ABC中,点E、F、G分别在边BC、AC、AB上,且$\frac{AG}{GB}$=$\frac{BE}{EC}$=$\frac{CF}{FA}$=$\frac{1}{2}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.
如图,△ABC中,点E、F、G分别在边BC、AC、AB上,且$\frac{AG}{GB}$=$\frac{BE}{EC}$=$\frac{CF}{FA}$=$\frac{1}{2}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
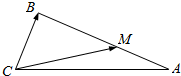 如图,在△ABC中,|$\overrightarrow{CA}$|=6,|$\overrightarrow{CB}$|=3,M为线段AB上的一点,且|$\overrightarrow{CM}$|=x•$\overrightarrow{CA}$+y•$\overrightarrow{CB}$,$\overrightarrow{BM}$=2$\overrightarrow{MA}$.
如图,在△ABC中,|$\overrightarrow{CA}$|=6,|$\overrightarrow{CB}$|=3,M为线段AB上的一点,且|$\overrightarrow{CM}$|=x•$\overrightarrow{CA}$+y•$\overrightarrow{CB}$,$\overrightarrow{BM}$=2$\overrightarrow{MA}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<n<m | B. | n<m<0 | C. | 0<m<n | D. | m<n<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com