
分析 (I)由已知可得:b=1,结合直线与圆M:x2+y2-4x-2y+4=0相切.进而可得c2=3,a2=4,即得椭圆C的标准方程;
(Ⅱ)在x轴上是否存在一点T(4,0),使得不论直线l的斜率如何变化,总有∠OTA=∠OTB,联立直线与椭圆方程,结合∠OTA=∠OTB 时,直线TA,TB的斜率k1,k2和为0,可证得结论.
解答 解:(I)由已知中椭圆C的短轴长为2,可得:b=1,
则过上顶点E(0,1)和右焦点F(0,c)的直线方程为:$\frac{x}{c}+y=1$,
即x+cy-c=0,
由直线与圆M:x2+y2-4x-2y+4=0相切.
故圆心M(2,1)到直线的距离d等于半径1,
即$\frac{|2+c-c|}{\sqrt{1+{c}^{2}}}=1$,
解得:c2=3,
则a2=4,
故椭圆C的标准方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)设A(x1,y1),B(x2,y2),
当直线AB的斜率不为0时,设直线 方程为:x=my+1,代入$\frac{{x}^{2}}{4}+{y}^{2}=1$得:(m2+4)y2+2my-3=0,
则y1+y2=$\frac{-2m}{{m}^{2}+4}$,y1•y2=$\frac{-3}{{m}^{2}+4}$,
设直线TA,TB的斜率分别为k1,k2,
若∠OTA=∠OTB,
则k1+k2=$\frac{{y}_{1}}{{x}_{1}-t}$+$\frac{{y}_{2}}{{x}_{2}-t}$=$\frac{{y}_{1}({x}_{2}-t)+{y}_{2}({x}_{1}-t)}{({x}_{1}-t)({x}_{2}-t)}$=$\frac{{y}_{1}({my}_{2}+1-t)+{y}_{2}({my}_{1}+1-t)}{({x}_{1}-t)({x}_{2}-t)}$
=$\frac{{2y}_{1}{y}_{2}m+({y}_{1}+{y}_{2})(1-t)}{({x}_{1}-t)({x}_{2}-t)}$=0,
即2y1y2m+(y1+y2)(1-t)=$\frac{-6m}{{m}^{2}+4}$+$\frac{-2m(1-t)}{{m}^{2}+4}$=0,
解得:t=4,
当直线AB的斜率为0时,t=4也满足条件,
综上,在x轴上存在一点T(4,0),使得不论直线l的斜率如何变化,总有∠OTA=∠OTB.
点评 本题考查的知识点是椭圆的标准方程,椭圆与直线的位置关系,难度中档.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $1-\frac{π}{6}$ | D. | $1-\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,3) | B. | [-2,3) | C. | (-2,3] | D. | [-2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
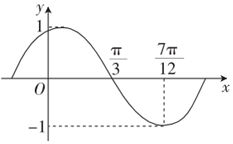 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),其部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),其部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com