
分析 (Ⅰ)利用任意角的三角函数定义,求出角的正弦函数与余弦函数值,利用诱导公式化简$\frac{{cos(α-\frac{π}{2})sin(2π-α)cos(π-α)}}{{sin(\frac{π}{2}+α)}}$,代入求解即可;
(Ⅱ)利用二倍角公式求出正弦函数与余弦函数值,然后利用两角和与差的三角函数化简求解即可.
解答 (本小题满分12分)
解:因为P(-4,3)为角α终边上一点,所以$sinα=\frac{3}{5}$,$cosα=-\frac{4}{5}$.…(2分)
(I)$\frac{{cos(α-\frac{π}{2})sin(2π-α)cos(π-α)}}{{sin(\frac{π}{2}+α)}}$
=$\frac{sinα•(-sinα)•(-cosα)}{cosα}$
=sin2α…(5分)
=$\frac{9}{25}$;…(6分)
(II)$sin2α=2sinαcosα=-\frac{24}{25}$,$cos2α=2{cos^2}α-1=\frac{7}{25}$,…(8分)
又因β为第三象限角,且tanβ=1,所以$sinβ=cosβ=-\frac{{\sqrt{2}}}{2}$,…(9分)
则cos(2α-β)=cos2αcosβ+sin2αsinβ…(10分)
=$\frac{7}{25}$×$(-\frac{{\sqrt{2}}}{2})$$+(-\frac{24}{25})×(-\frac{{\sqrt{2}}}{2})$=$\frac{{17\sqrt{2}}}{50}$.…(12分)
点评 本题考查两角和与差的三角函数,三角函数的定义,诱导公式的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
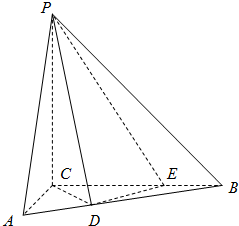 三棱锥P-ABC中,PC⊥平面ABC,PC=6,BC⊥AC,D,E分别是线段AB.BC上的点,且CD=DE=2$\sqrt{2}$,CE=2EB=4
三棱锥P-ABC中,PC⊥平面ABC,PC=6,BC⊥AC,D,E分别是线段AB.BC上的点,且CD=DE=2$\sqrt{2}$,CE=2EB=4查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{sin0.5}$ | B. | sin0.5 | C. | 2sin1 | D. | $\frac{1}{cos0.5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com