
分析 利用复数代数形式的乘除运算分别化简括号内部的代数式,然后利用复数代数形式的乘除运算化简求得答案.
解答 解:∵$\frac{2+2i}{\sqrt{3}-i}=\frac{(2+2i)(\sqrt{3}+i)}{(\sqrt{3}-i)(\sqrt{3}+i)}=\frac{2\sqrt{3}-2+(2\sqrt{3}+2)i}{4}$=$\frac{\sqrt{3}-1}{2}+\frac{\sqrt{3}+1}{2}i$=$\frac{1}{2}(1+i)(\sqrt{3}+i)$,
$\frac{2-2i}{1+\sqrt{3}i}=\frac{(2-2i)(1-\sqrt{3}i)}{(1+\sqrt{3}i)(1-\sqrt{3}i)}=\frac{2-2\sqrt{3}-(2\sqrt{3}+2)i}{4}$=$\frac{1-\sqrt{3}}{2}-\frac{\sqrt{3}+1}{2}i$=$-\frac{1}{2}(1+i)(\sqrt{3}+i)$,
∴($\frac{2+2i}{\sqrt{3}-i}$)7-($\frac{2-2i}{1+\sqrt{3}i}$)7=$\frac{1}{{2}^{6}}(1+i)^{7}(\sqrt{3}+i)^{7}$.
∵(1+i)2=2i,∴(1+i)7=(2i)3(1+i)=8-8i,
∵$(\sqrt{3}+i)^{2}=2+2\sqrt{3}i$,∴$(\sqrt{3}+i)^{7}=-64\sqrt{3}-64i$,
∴原式=$\frac{1}{64}(8-8i)(-64\sqrt{3}-64i)=(-8\sqrt{3}-8)+(8\sqrt{3}-8)i$.
故答案为:$(-8\sqrt{3}-8)+(8\sqrt{3}-8)i$.
点评 本题考查了复数代数形式的混合运算,考查了学生灵活的计算能力,是中档题.


科目:高中数学 来源: 题型:选择题
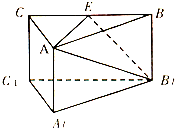 如图,三棱柱中,侧棱AA1⊥底面A1B1C1,三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱中,侧棱AA1⊥底面A1B1C1,三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | A1C1⊥平面ABB1A1 | ||
| C. | AE,B1C1为异面直线,且AE⊥B1C1 | D. | A1C1∥平面A1EB |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,过圆外一点P作直线AB的垂线,垂足为F,交圆于C,E两点,PD切圆于D,连接AD交EP于G.
如图,过圆外一点P作直线AB的垂线,垂足为F,交圆于C,E两点,PD切圆于D,连接AD交EP于G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是等边三角形,平面PAD⊥平面ABCD,M,N分别是棱PC,AB的中点,且MN⊥CD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是等边三角形,平面PAD⊥平面ABCD,M,N分别是棱PC,AB的中点,且MN⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | ($\frac{4}{3}$,0) | C. | ($\frac{5}{3}$,0) | D. | (2,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com