
���� ��1���������=$[\begin{array}{l}{a}&{2}\\{b}&{-1}\end{array}]$ $[\begin{array}{l}{3}\\{1}\end{array}]$=$[\begin{array}{l}{3a+2}\\{3b-1}\end{array}]$=$[\begin{array}{l}{5}\\{-1}\end{array}]$����$\left\{\begin{array}{l}{3a+2=5}\\{3b-1=-1}\end{array}\right.$��������ɵó�A��det��A��=$|\begin{array}{l}{1}&{2}\\{0}&{-1}\end{array}|$=-1�����ɵó�A�������A-1��
��2��ԲC����ͨ����Ϊ��x-m��2+y2=4��ֱ��l�ļ����귽�̻�Ϊ�� ��$\frac{\sqrt{2}}{2}$cos��+$\frac{\sqrt{2}}{2}$sin�ȣ�=$\sqrt{2}$�����û�����ʽ�ɵã�ֱ�����귽�̣����õ㵽ֱ�ߵľ��빫ʽ����ֱ����Բ���ཻ�ij�Ҫ�������ɵó���
��� �⣺��1���������=$[\begin{array}{l}{a}&{2}\\{b}&{-1}\end{array}]$ $[\begin{array}{l}{3}\\{1}\end{array}]$=$[\begin{array}{l}{3a+2}\\{3b-1}\end{array}]$=$[\begin{array}{l}{5}\\{-1}\end{array}]$��
��$\left\{\begin{array}{l}{3a+2=5}\\{3b-1=-1}\end{array}\right.$�����$\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$��
��A=$[\begin{array}{l}{1}&{2}\\{0}&{-1}\end{array}]$��
��det��A��=$|\begin{array}{l}{1}&{2}\\{0}&{-1}\end{array}|$=1����-1��-0��2=-1��
��A�������A-1=$[\begin{array}{l}{1}&{2}\\{0}&{-1}\end{array}]$��
��2��ԲC�IJ�������Ϊ$\left\{\begin{array}{l}x=m+2cos��\\ y=2sin��\end{array}$����Ϊ������mΪ������������ƽ����ϵ�ɵã�ԲC����ͨ����Ϊ��x-m��2+y2=4��
ֱ��l�ļ����귽�̻�Ϊ�� ��$\frac{\sqrt{2}}{2}$cos��+$\frac{\sqrt{2}}{2}$sin�ȣ�=$\sqrt{2}$��
��$\frac{\sqrt{2}}{2}$x+$\frac{\sqrt{2}}{2}$y=$\sqrt{2}$�������x+y-2=0��
��ԲC��Բ��ΪC��m��0�����뾶Ϊ2��Բ��C��ֱ��l�ľ���d=$\frac{|m-2|}{\sqrt{2}}$��
��d=$\frac{|m-2|}{\sqrt{2}}$��2��
���2-2$\sqrt{2}$��m��2+2$\sqrt{2}$��
���� ���⿼���˾���任������ʽ�ļ��㡢�����귽�̻�Ϊֱ�����귽�̡��������̻�Ϊ��ͨ���̡��㵽ֱ�ߵľ��빫ʽ��ֱ����Բ��λ�ù�ϵ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | -15 | D�� | 15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
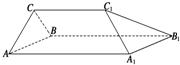 ��ͼ��ʾ�ļ������У��ı���AA1B1B�DZ߳�Ϊ3�������Σ�CC1=2��CC1��AA1����������������������ǣ�ָ���Ǽ���������������������������һ��ƽ���ȥһ���֣�ʹʣ�ಿ����һ���ⳤΪ2������������ָ����ȥ�ļ������������������ͼ�л������森
��ͼ��ʾ�ļ������У��ı���AA1B1B�DZ߳�Ϊ3�������Σ�CC1=2��CC1��AA1����������������������ǣ�ָ���Ǽ���������������������������һ��ƽ���ȥһ���֣�ʹʣ�ಿ����һ���ⳤΪ2������������ָ����ȥ�ļ������������������ͼ�л������森�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
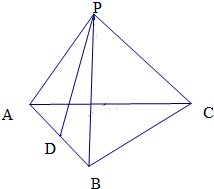 ��ͼ������P-ABC���ⳤ����ȣ�D����AB���е㣬��ֱ��PD��ֱ��BC���ɽǵ�����ֵΪ��������
��ͼ������P-ABC���ⳤ����ȣ�D����AB���е㣬��ֱ��PD��ֱ��BC���ɽǵ�����ֵΪ��������| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{3}}{3}$ | C�� | $\frac{\sqrt{3}}{6}$ | D�� | $\frac{\sqrt{6}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
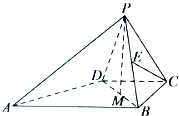 ��ͼ������P-ABCD�У���ABC=��BCD=90�㣬AB=2��CD=CB=CP=1����P�ڵ����ϵ���ӰΪ�߶�BD���е�M��
��ͼ������P-ABCD�У���ABC=��BCD=90�㣬AB=2��CD=CB=CP=1����P�ڵ����ϵ���ӰΪ�߶�BD���е�M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 2 | C�� | 1 | D�� | 0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com