
【题目】已知等差数列{an}的前n项和为Sn , 等比数列{bn}的前n项和为Tn , a1=﹣1,b1=1,a2+b2=2.
(Ⅰ)若a3+b3=5,求{bn}的通项公式;
(Ⅱ)若T3=21,求S3 .
【答案】解:(Ⅰ)设等差数列{an}的公差为d,等比数列{bn}的公比为q,
a1=﹣1,b1=1,a2+b2=2,a3+b3=5,
可得﹣1+d+q=2,﹣1+2d+q2=5,
解得d=1,q=2或d=3,q=0(舍去),
则{bn}的通项公式为bn=2n﹣1 , n∈N*;
(Ⅱ)b1=1,T3=21,
可得1+q+q2=21,
解得q=4或﹣5,
当q=4时,b2=4,a2=2﹣4=﹣2,
d=﹣2﹣(﹣1)=﹣1,S3=﹣1﹣2﹣3=﹣6;
当q=﹣5时,b2=﹣5,a2=2﹣(﹣5)=7,
d=7﹣(﹣1)=8,S3=﹣1+7+15=21.
【解析】(Ⅰ)设等差数列{an}的公差为d,等比数列{bn}的公比为q,运用等差数列和等比数列的通项公式,列方程解方程可得d,q,即可得到所求通项公式;
(Ⅱ)运用等比数列的求和公式,解方程可得公比,再由等差数列的通项公式和求和,计算即可得到所求和.
【考点精析】解答此题的关键在于理解等差数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() 或
或![]() ,以及对等差数列的前n项和公式的理解,了解前n项和公式:
,以及对等差数列的前n项和公式的理解,了解前n项和公式:![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,异面直线A1B与B1C1所成的角为60°.
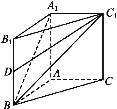
(1)求该三棱柱的体积;
(2)设D是BB1的中点,求DC1与平面A1BC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将![]() 沿AB折到
沿AB折到![]() 的位置,使
的位置,使![]() ,点E在SD上,且
,点E在SD上,且![]() ,如下图。
,如下图。
(1)求证: ![]() 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.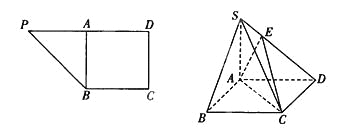
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4![]() .
.
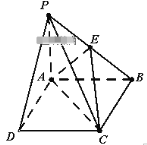
(I)求证:PD∥面ACE;
(Ⅱ)求三棱锥E﹣ABC的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A﹣BD﹣E与二面角E﹣BD﹣C′的大小分别为15°和30°,则![]() __.
__.
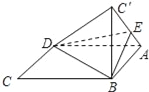
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com