
分析 (1)要证函数在(1,+∞)上是增函数,只需要证明其导数大于0即可;
(2)求导函数先研究函数的单调性,确定极值,从而确定函数的最值,分类讨论是解题的关键
解答 解:(1)当a=2时,f(x)=x2-2lnx,
∴f′(x)=$\frac{2{(x}^{2}-1)}{x}$>0,
令f′(x)>0,解得:x>1,
令f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
∴f(x)极小值=f(1)=1.
(2)解:f′(x)=$\frac{{2x}^{2}-a}{x}$(x>0),
当x∈[1,e],2x2-a∈[2-a,2e2-a].
若a≤2,则当x∈[1,e]时,f′(x)≥0,
所以f(x)在[1,e]上是增函数,
又f(1)=1,故函数f(x)在[1,e]上的最小值为1.
若a≥2e2,则当x∈[1,e]时,f′(x)≤0,
所以f(x)在[1,e]上是减函数,
又f(e)=e2-a,所以f(x)在[1,e]上的最小值为e2-a.
若2<a<2e2,则当1≤x<$\sqrt{\frac{a}{2}}$时,f′(x)<0,此时f(x)是减函数;
当$\sqrt{\frac{a}{2}}$<x≤e时,f′(x)>0,此时f(x)是增函数.
又f($\sqrt{\frac{a}{2}}$)=$\frac{a}{2}$-$\frac{a}{2}$ln$\frac{a}{2}$,
所以f(x)在[1,e]上的最小值为$\frac{a}{2}$-$\frac{a}{2}$ln$\frac{a}{2}$.
综上可知,当a≤2时,f(x)在[1,e]上的最小值为1;
当2<a<2e2时,f(x)在[1,e]上的最小值为$\frac{a}{2}$-$\frac{a}{2}$ln$\frac{a}{2}$;
当a≥2e2时,f(x)在[1,e]上的最小值为e2-a,
综上:f(x)min=$\left\{\begin{array}{l}{1,a≤2}\\{\frac{a}{2}(1-ln\frac{a}{2}),2<a<{2e}^{2}}\\{{e}^{2}-a,a>{2e}^{2}}\end{array}\right.$.
点评 本题以函数为载体,考查函数的单调性与函数的最值.利用导数研究函数的单调性比用函数单调性的定义要方便,但应注意f′(x)>0(或f′(x)<0)仅是f(x)在某个区间上为增函数(或减函数)的充分条件.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既没有最大值也没有最小值 | B. | 有最大值5,没有最小值 | ||
| C. | 有最小值-1,没有最大值 | D. | 有最小值-5,也有最大值5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,4) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{1}{4}$,$\frac{1}{2}$) | D. | ($\frac{1}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{1}{10}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2),3 | B. | (-1,2),9 | C. | (1,-2),3 | D. | (1,-2),9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
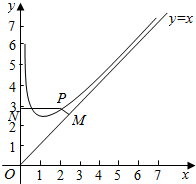 已知函数f(x)=x+$\frac{a}{x}$ (x>0)的最小最小值为$2•\root{4}{2}$,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
已知函数f(x)=x+$\frac{a}{x}$ (x>0)的最小最小值为$2•\root{4}{2}$,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com