
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由条件利用两个向量的数量积的运算法则和性质逐一判断各个选项是否正确,从而得出结论.
解答 解:由于两个向量的数量积为实数,故①错误;
由于实数与向量的乘积还是向量,故②错误;
根据两个向量的减法的法则和几何意义,$\overrightarrow{0}$-$\overrightarrow{AB}$=-$\overrightarrow{AB}$=$\overrightarrow{BA}$,故③正确;
由于|$\overrightarrow{a}$•$\overrightarrow{b}$|=||$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cosθ|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•|cosθ|,故④错误;
($\overrightarrow{a}$•$\overrightarrow{b}$)2=${(|\overrightarrow{a}|•|\overrightarrow{b}|•cosθ)}^{2}$,故⑤错误;
若$\overrightarrow{a}$与$\overrightarrow{b}$是两个单位向量,则$\overrightarrow{{a}^{2}}$=$\overrightarrow{{b}^{2}}$=1,故⑥正确;
⑦若$\overrightarrow{a}$⊥($\overrightarrow{b}$-$\overrightarrow{c}$),则$\overrightarrow{a}$•($\overrightarrow{b}$-$\overrightarrow{c}$)=$\overrightarrow{a}$•$\overrightarrow{b}$-$\overrightarrow{a}$•$\overrightarrow{c}$=0,即$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,故⑦正确,
故选:C.
点评 本题主要考查两个向量的数量积的运算法则和性质,属于基础题.


科目:高中数学 来源:2016-2017学年安徽六安一中高二上文周末检测三数学试卷(解析版) 题型:解答题
已知函数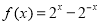 ,数列
,数列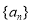 满足
满足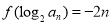 .
.
(1)求数列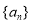 的通项公式;
的通项公式;
(2)证明:数列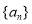 是递减数列.
是递减数列.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{22}}{14}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{3\sqrt{22}}{14}$或$\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上文周末检测三数学试卷(解析版) 题型:选择题
若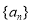 是等差数列,下列数列中仍为等差数列的有( )
是等差数列,下列数列中仍为等差数列的有( )
①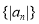 ;
;
②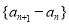 ;
;
③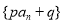 (
( ,
,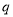 为常数);
为常数);
④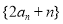 .
.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com