Question

4．函数f（x）=$\frac{\sqrt{{x}^{2}-{x}^{4}}}{|x-2|-2}$．给出函数f（x）下列性质：
（1）函数的定义域和值域均为[-1，1]；
（2）函数的图象关于原点成中心对称；
（3）函数在定义域上单调递增；
（4）A、B为函数f（x）图象上任意不同两点，则$\sqrt{2}$＜|AB|≤2．
请写出所有关于函数f（x）性质正确描述的序号（2）．

Answer 1

分析 化简函数f（x），画出函数f（x）的图象，结合图象，对选项中的命题进行分析判断即可．

解答 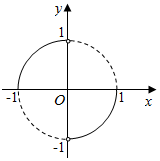解：∵函数f（x）=$\frac{\sqrt{{x}^{2}-{x}^{4}}}{|x-2|-2}$，
∴$\left\{\begin{array}{l}{{x}^{2}{-x}^{4}≥0}\\{|x-2|-2≠0}\end{array}\right.$，
解得-1≤x≤1且x≠0，
∴函数f（x）的定义域为[-1，0）∪（0，1]，（1）错误；
∵f（x）=$\frac{\sqrt{{x}^{2}{-x}^{4}}}{|x-2|-2}$=$\left\{\begin{array}{l}{\sqrt{1{-x}^{2}}，-1≤x＜0}\\{-\sqrt{1{-x}^{2}}，0＜x≤1}\end{array}\right.$
作出函数f（x）图象，如图所示；
由图象知函数f（x）的图象关于原点成中心对称，（2）正确；
由图象知函数f（x）在[-1，0）上为单调增函数，在（0，1]上也是单调增函数，
但在定义域[-1，0）∪（0，1]上不是增函数，
如-1＜1，但f（-1）=f（1）=0，故（3）错误；
由图象知图象为两个四分之一个圆弧构成，且半径为1，
最大为AB连线且过原点，最大值为2，最小为AB是0，但取不到，即0＜|AB|≤2，故（4）错误．
综上，正确的命题是（2）．
故答案为：（2）．

点评 本题考查了分段函数的图象与性质的应用问题，也考查了函数的定义域和值域的应用问题，是综合性题目．