
【题目】如图,已知![]() 是圆柱
是圆柱![]() 底面圆O的直径,底面半径
底面圆O的直径,底面半径![]() ,圆柱的表面积为
,圆柱的表面积为![]() ,点
,点![]() 在底面圆
在底面圆![]() 上,且直线
上,且直线![]() 与下底面所成的角的大小为
与下底面所成的角的大小为![]() .
.
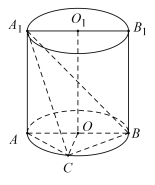
(1)求![]() 的长;
的长;
(2)求二面角![]() 的大小的余弦值.
的大小的余弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据母线![]() 底面
底面![]() ,即可找出
,即可找出![]() 与下底面所成的角的为
与下底面所成的角的为![]() ,从而在直角三角形
,从而在直角三角形![]() 中,即可求出
中,即可求出![]() ;
;
(2) 以![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 分别为
分别为![]() 、
、![]() 轴建立空间直角坐标系,写出所需点的坐标,分别求出平面
轴建立空间直角坐标系,写出所需点的坐标,分别求出平面![]() 和平面
和平面![]() 的法向量,利用向量的夹角公式,即可求得二面角
的法向量,利用向量的夹角公式,即可求得二面角![]() 的大小的余弦值.
的大小的余弦值.
(1)设圆柱的母线长为![]() ,则根据已知条件可得,
,则根据已知条件可得,
![]() ,
,![]() ,解得
,解得![]() ,因为
,因为![]() 底面
底面![]() ,所以
,所以![]() 是
是![]() 在底面
在底面![]() 上的射影,所以
上的射影,所以![]() 是直线
是直线![]() 与下底面
与下底面![]() 所成的角,即
所成的角,即![]()
在直角三角形![]() 中,
中,![]() ,
,![]()
![]()
![]() ,
,![]()
(2)因为![]() 是底面直径,
是底面直径,![]() ,所以
,所以![]()
以![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 分别为
分别为![]() 、
、![]() 轴建立空间直角坐标系,如图所示,
轴建立空间直角坐标系,如图所示,
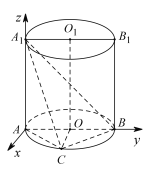
则![]() 、
、![]() 、
、![]() 、
、![]() ,
,
于是![]() ,
,![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则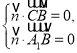 即
即 不妨令
不妨令![]() ,即平面
,即平面![]() 的一个法向量
的一个法向量![]() ,
,
因为平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,则
,则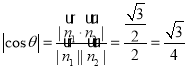 ,
,
由于二面角![]() 为锐角,所以二面角
为锐角,所以二面角![]() 的大小的余弦值是
的大小的余弦值是![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|x﹣a+1|.
(1)当a=4时,求解不等式f(x)≥8;
(2)已知关于x的不等式f(x)![]() 在R上恒成立,求参数a的取值范围.
在R上恒成立,求参数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.曲线
轴正半轴为极轴建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程,曲线
的普通方程,曲线![]() 的参数方程;
的参数方程;
(2)若![]() 分别为曲线
分别为曲线![]() ,
,![]() 上的动点,求
上的动点,求![]() 的最小值,并求
的最小值,并求![]() 取得最小值时,
取得最小值时,![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与上下顶点构成直角三角形,以椭圆E的长轴为直径的圆与直线
的一个焦点与上下顶点构成直角三角形,以椭圆E的长轴为直径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)![]() 为椭圆
为椭圆![]() 上不同的三点,
上不同的三点,![]() 为坐标原点,若
为坐标原点,若![]() ,试问:
,试问:![]() 的面积是否为定值?若是,请求出定值;若不是,请说明理由.
的面积是否为定值?若是,请求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
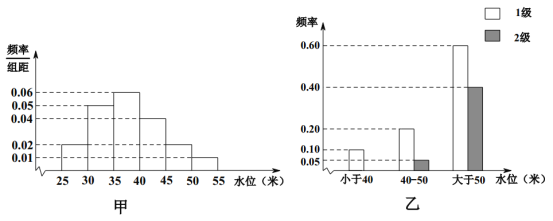
(1)试估计该河流在8月份水位的众数;
(2)我们知道若该河流8月份的水位小于40米的频率为f,该河流8月份的水位小于40米的情况下发生1级灾害的频率为g,则该河流8月份的水位小于40且发生1级灾害的频率为![]() ,其他情况类似.据此,试分别估计该河流在8月份发生12级灾害及不发生灾害的频率
,其他情况类似.据此,试分别估计该河流在8月份发生12级灾害及不发生灾害的频率![]() ,
,![]() ,
,![]() ;
;
(3)该河流域某企业,在8月份,若没受12级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() ,…,
,…,![]() 的项
的项![]() ,其中
,其中![]() …,
…,![]() ,
,![]() ,其前
,其前![]() 项和为
项和为![]() ,记
,记![]() 除以3余数为1的数列
除以3余数为1的数列![]() ,
,![]() ,…,
,…,![]() 的个数构成的数列为
的个数构成的数列为![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)求数列![]() 的通项公式,并化简.
的通项公式,并化简.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为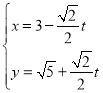 (
(![]() 为参数)。在极坐标系(与直角坐标系
为参数)。在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com