
|
|
|
|
| 2 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 一次期末考试,学校随机抽取了一批学生的物理成绩(满分100分),经统计,这批抽取的学生的成绩全部介于65分到100分之间,现将数据分成以下7组:第1组[65,70],第2组[70,75],第3组[75,80],第4组[80.85],第5组[85,90],第6组[90,95],第7组[95,100],得到如图所示的频率分布直方图(不完整).
一次期末考试,学校随机抽取了一批学生的物理成绩(满分100分),经统计,这批抽取的学生的成绩全部介于65分到100分之间,现将数据分成以下7组:第1组[65,70],第2组[70,75],第3组[75,80],第4组[80.85],第5组[85,90],第6组[90,95],第7组[95,100],得到如图所示的频率分布直方图(不完整).查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
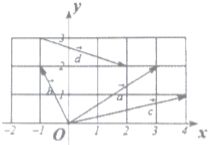 如图所示,在平面直角坐标系xOy中,取x轴、y轴正方向上的单位向量为基底.
如图所示,在平面直角坐标系xOy中,取x轴、y轴正方向上的单位向量为基底.| a |
| b |
| c |
| d |
| a |
| c |
| b |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| sin(α-3π)•cos(π+α) | ||
cos(2π-α)•sin(-π-α)•sin(
|
| 3π |
| 2 |
| 1 |
| 3 |
| 34 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点.
如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点.| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com