
���� ��1���ѵ�$P��\;\frac{{\sqrt{6}}}{2}\;��\;\frac{1}{2}\;��$������Բ���̿ɵ�$\frac{{{{��\;\frac{{\sqrt{6}}}{2}\;��}^2}}}{a^2}+\frac{{{{��\;\frac{1}{2}\;��}^2}}}{b^2}=1$����$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$��a2=b2+c2������������ɵó���
��2����OMΪֱ����Բ��Բ��Ϊ$��\;1\;��\;\frac{t}{2}\;��$���뾶$r=\sqrt{\frac{t^2}{4}+1}$���ɵ�Բ�ı����̣�������OMΪֱ����Բ��ֱ��3x-4y-5=0�صõ��ҳ�Ϊ2�����õ㵽ֱ�ߵľ��빫ʽ�ɵ�Բ�ĵ�ֱ��3x-4y-5=0�ľ���d�������ҳ���ʽ�ɵ��ҳ�=2$\sqrt{{r}^{2}-{d}^{2}}$���ɵó���
��3������һ������F��OM�Ĵ��ߣ�������ΪK��ֱ��OM�ķ���Ϊ$y=\frac{t}{2}x$��ֱ��FN�ķ���Ϊ$y=-\frac{2}{t}��x-1��$���������K���꣬�ɵ�|OK|��|OM|������|ON|2=|OK|•|OM|����֤����
����������N��x0��y0������$\overrightarrow{FN}=��\;{x_0}-1\;��\;{y_0}\;��$��$\overrightarrow{OM}=��\;2\;��\;t\;��$��$\overrightarrow{MN}=��\;{x_0}-2\;��\;{y_0}-t\;��$��$\overrightarrow{ON}=��\;{x_0}\;��\;{y_0}\;��$������$\overrightarrow{FN}��\overrightarrow{OM}$��$\overrightarrow{MN}��\overrightarrow{ON}$����֤$|ON|=\sqrt{{x}_{0}^{2}+{y}_{0}^{2}}$Ϊ��ֵ��
��� ��1���⣺�������$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$����
����Բ������$P��\;\frac{{\sqrt{6}}}{2}\;��\;\frac{1}{2}\;��$����$\frac{{{{��\;\frac{{\sqrt{6}}}{2}\;��}^2}}}{a^2}+\frac{{{{��\;\frac{1}{2}\;��}^2}}}{b^2}=1$��
��a2=b2+c2��
�ɢ٢ڢ۽��a2=2��b2=c2=1��
����Բ�ķ���Ϊ$\frac{x^2}{2}+{y^2}=1$��
��2���⣺��OMΪֱ����Բ��Բ��Ϊ$��\;1\;��\;\frac{t}{2}\;��$���뾶$r=\sqrt{\frac{t^2}{4}+1}$��
��Բ�ķ���Ϊ${��x-1��^2}+{��y-\frac{t}{2}��^2}=\frac{t^2}{4}+1$��
����OMΪֱ����Բ��ֱ��3x-4y-5=0�صõ��ҳ�Ϊ2��
��Բ�ĵ�ֱ��3x-4y-5=0�ľ���$d=\sqrt{{r^2}-1}=\sqrt{\frac{t^2}{4}+1-1}=\frac{t}{2}$��
��$\frac{|3-2t-5|}{5}=\frac{t}{2}$����2|2t+2|=5t��
��4t+4=5t����4t+4=-5t��
���t=4����$t=-\frac{4}{9}$��
��t��0����t=4��
����Բ�ķ���Ϊ��x-1��2+��y-2��2=5��
��3��֤��������һ������F��OM�Ĵ��ߣ�������ΪK��
ֱ��OM�ķ���Ϊ$y=\frac{t}{2}x$��ֱ��FN�ķ���Ϊ$y=-\frac{2}{t}��x-1��$��
��$\left\{\begin{array}{l}y=\frac{t}{2}x\\ y=-\frac{2}{t}��x-1��\end{array}\right.$�����$x=\frac{4}{{{t^2}+4}}$����$K��\;\frac{4}{{{t^2}+4}}\;��\;\frac{2t}{{{t^2}+4}}\;��$��
��$|OK|\;=\sqrt{\frac{16}{{{{��{t^2}+4��}^2}}}+\frac{{4{t^2}}}{{{{��{t^2}+4��}^2}}}}=\sqrt{\frac{4}{{{t^2}+4}}}$��
$|OM|\;=\sqrt{4+{t^2}}$��
��$|ON{|^2}\;=\;|OK|•|OM|\;=\sqrt{\frac{4}{{4+{t^2}}}}•\sqrt{4+{t^2}}=2$��
��$|ON|\;=\sqrt{2}$��
���߶�ON�ij�Ϊ��ֵ$\sqrt{2}$��
����������N��x0��y0������$\overrightarrow{FN}=��\;{x_0}-1\;��\;{y_0}\;��$��$\overrightarrow{OM}=��\;2\;��\;t\;��$��$\overrightarrow{MN}=��\;{x_0}-2\;��\;{y_0}-t\;��$��$\overrightarrow{ON}=��\;{x_0}\;��\;{y_0}\;��$��
��$\overrightarrow{FN}��\overrightarrow{OM}$����2��x0-1��+ty0=0����2x0+ty0=2��
�֡�$\overrightarrow{MN}��\overrightarrow{ON}$����x0��x0-2��+y0��y0-t��=0��
��$x_0^2+y_0^2=2{x_0}+t{y_0}=2$��
��$|\overrightarrow{ON}|\;=\sqrt{x_0^2+y_0^2}=\sqrt{2}$Ϊ��ֵ��
���� ���⿼����Բ���ߵı����̼������ʡ�ֱ������Բ��Բ���ཻ���⡢������ֱ��������֮��Ĺ�ϵ���ҳ���ʽ���㵽ֱ�ߵľ��빫ʽ�Ȼ���֪ʶ��������ܣ���������������������������������⣮


 С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
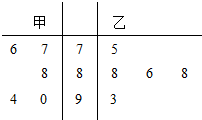 �ڡ������ڽ���ѡ�����У��ס�����λ���ֵ�5�ε÷�����羥Ҷͼ��ʾ���Ǽס������˵�ƽ���÷ֱַ�$\overline{{X}_{��}}$��$\overline{{X}_{��}}$���������ж���ȷ���ǣ�������
�ڡ������ڽ���ѡ�����У��ס�����λ���ֵ�5�ε÷�����羥Ҷͼ��ʾ���Ǽס������˵�ƽ���÷ֱַ�$\overline{{X}_{��}}$��$\overline{{X}_{��}}$���������ж���ȷ���ǣ�������| A�� | $\overline{{X}_{��}}$��$\overline{{X}_{��}}$���ұȼ׳ɼ��ȶ� | B�� | $\overline{{X}_{��}}$��$\overline{{X}_{��}}$���ױ��ҳɼ��ȶ� | ||
| C�� | $\overline{{X}_{��}}$��$\overline{{X}_{��}}$���ױ��ҳɼ��ȶ� | D�� | $\overline{{X}_{��}}$��$\overline{{X}_{��}}$���ұȼ׳ɼ��ȶ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
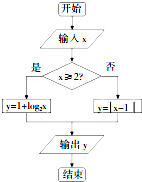 ��ͼ�����ͼ����������κ�һ��ȷ����yֵʱǡ��ֻ��Ӧ����Ψһ��xֵ�������������yֵ�ķ�Χ��[0��+�ޣ���
��ͼ�����ͼ����������κ�һ��ȷ����yֵʱǡ��ֻ��Ӧ����Ψһ��xֵ�������������yֵ�ķ�Χ��[0��+�ޣ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
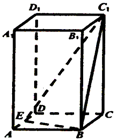 ��֪��������ABCD-A1B1C1D1�ĵ���߳�Ϊ2�����ⳤΪ����߳���2����E��ΪAD���е㣬������D-BEC1�����Ϊ��������
��֪��������ABCD-A1B1C1D1�ĵ���߳�Ϊ2�����ⳤΪ����߳���2����E��ΪAD���е㣬������D-BEC1�����Ϊ��������| A�� | $\frac{8}{3}$ | B�� | 4 | C�� | $\frac{4}{3}$ | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{{\sqrt{2}}}{3}$ | C�� | $\frac{{\sqrt{6}}}{3}$ | D�� | $\frac{{\sqrt{3}}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2\sqrt{34}}{17}$ | B�� | $\frac{\sqrt{6}}{3}$ | C�� | $\frac{4\sqrt{7}}{7}$ | D�� | $\frac{4}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com