
| 女 | 47 36 32 48 34 44 43 47 46 41 43 42 50 43 35 49 |
| 男 | 37 35 34 43 46 36 38 40 39 32 48 33 40 34 |
| “满意”的人数 | “不满意”人数 | 合计 | |
| 女 | 16 | ||
| 男 | 14 | ||
| 合计 | 30 |
分析 (1)求出任选一名员工,它的得分大于45分的概率,即可估计该企业得分大于45分的员工人数;
(2)根据所给数据,可得2×2列联表;
(3)求出k,与临界值比较,即可得出能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关.
解答 解:(1)从表中可知,3名员工中有8名得分大于45分,
∴任选一名员工,它的得分大于45分的概率是$\frac{8}{30}$=$\frac{4}{15}$,
∴估计此次调查中,该单位共有900×$\frac{4}{15}$=240名员工的得分大于45分; (4分)
(2)完成下列表格:
| “满意”的人数 | “不满意”人数 | 合计 | |
| 女 | 12 | 4 | 16 |
| 男 | 3 | 11 | 14 |
| 合计 | 15 | 15 | 30 |
点评 本题考查了古典概型,列联表,独立性检验的方法等知识,考查了学生处理数据和运算求解的能力.


科目:高中数学 来源: 题型:选择题
| A. | P1<P2 | B. | P1>P2 | ||
| C. | P1=P2 | D. | P1,P2大小不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
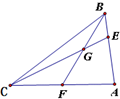 如图,在△ABC中,BE:EA=1:2,F是AC中点,线段CE与BF交于点G,则△BEG的面积与△ABC的面积之比是( )
如图,在△ABC中,BE:EA=1:2,F是AC中点,线段CE与BF交于点G,则△BEG的面积与△ABC的面积之比是( )| A. | $\frac{1}{16}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{2}$,$\frac{3π}{2}$) | B. | (π,2π) | C. | ($\frac{3π}{2}$,$\frac{5π}{2}$) | D. | (2π,3π) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| p(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
| A. | 25% | B. | 97.5% | C. | 5% | D. | 95% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com