
 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
 平面BDE,
平面BDE, 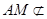 平面BDE,∴AM∥平面BDE.……4分
平面BDE,∴AM∥平面BDE.……4分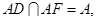 ∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,
∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,
 ∴二面角A—DF—B的大小为60º.……8分
∴二面角A—DF—B的大小为60º.……8分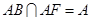 ,∴PQ⊥平面ABF,
,∴PQ⊥平面ABF, 平面ABF,∴PQ⊥QF.在RtΔPQF中,∠FPQ=60º,PF=2PQ.
平面ABF,∴PQ⊥QF.在RtΔPQF中,∠FPQ=60º,PF=2PQ. 又∵ΔPAF为直角三
又∵ΔPAF为直角三 ,∴
,∴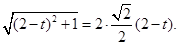 所以t=1或t=3(舍去),即点P是AC的中点.……12分
所以t=1或t=3(舍去),即点P是AC的中点.……12分 ,连接NE, 则点N、E的坐标分别是(
,连接NE, 则点N、E的坐标分别是( 、(0,0,1),
、(0,0,1),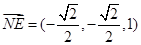 , 又点A、M的坐标分别是
, 又点A、M的坐标分别是 ,(
,(
 =(
=( ∴
∴ 且NE与AM不共线,∴NE∥AM.又∵
且NE与AM不共线,∴NE∥AM.又∵ 平面BDE,
平面BDE, 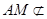 平面BDE,∴AM∥平面BDE.
平面BDE,∴AM∥平面BDE. ∴AB⊥平面ADF.
∴AB⊥平面ADF.
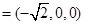 为平面DAF的法向量.
为平面DAF的法向量.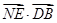 =(
=( ·
·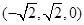 =0,
=0, =(
=( ·
· =0得
=0得 ,
, ,∴NE为平面BDF的法向量.
,∴NE为平面BDF的法向量.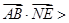 =
=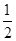 ∴AB与NE的夹角是60º.即所求二面角A—DF—B的大小是60º.
∴AB与NE的夹角是60º.即所求二面角A—DF—B的大小是60º. )得
)得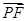
 ∴
∴ =(0,
=(0, , 0)
, 0)
 或
或 (舍去),即点P是AC的中点.
(舍去),即点P是AC的中点.

科目:高中数学 来源:不详 题型:单选题
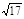 ,则这个二面角的大小为( )
,则这个二面角的大小为( )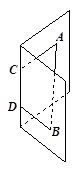
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①
是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:① ②
② ③
③ 如果命题
如果命题 且_______,则
且_______,则 为真命题,则可以在横线处填入的条件是( )
为真命题,则可以在横线处填入的条件是( )| A.①或② | B.②或③ | C.①或③ | D.只有② |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 ;
; ,求AB的长.
,求AB的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com