
 某手机生产企业为了解消费者对某款手机功能的认同情况,通过销售部随机抽取50名购买该款手机的消费者,并发出问卷调查,该问卷只有30份给予回复,这30份的评分如下:
某手机生产企业为了解消费者对某款手机功能的认同情况,通过销售部随机抽取50名购买该款手机的消费者,并发出问卷调查,该问卷只有30份给予回复,这30份的评分如下:| 男 | 47,36,28,48,29,48,44,50,46,46,42,45,50,37,35,49 |
| 女 | 38,35,37,48,47,36,38,45,39,29,49,28,44,33 |
| 满意 | 不满意 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.05 | 0.025 | 0.01 |
| k0 | 3.841 | 5.024 | 6.635 |
分析 (Ⅰ)由图可知男消费者评分的中位数是45.5,即可估计女性使用微信的平均时间;
(Ⅱ)列出列联表,求出K2,与临界值比较即可得出结论.
解答 解:(Ⅰ)茎叶图如图.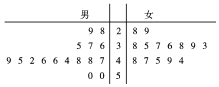
由图可知男消费者评分的中位数是45.5,
女消费者评分的平均值为$\frac{1}{14}({38+35+37+48}\right.$+47+36+38+45+39+29+49+28+44+33)=39.
(Ⅱ)列联表如图,
| 满意 | 不满意 | 合计 | |
| 男 | 11 | 5 | 16 |
| 女 | 5 | 9 | 14 |
| 合计 | 16 | 14 | 30 |
点评 本题主要考查独立性检验、茎叶图,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2e}$) | B. | (-∞,$\frac{1}{2e}$) | C. | ($\frac{1}{2e}$,+∞) | D. | ($\frac{1}{2e}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方体ABCD-A1B1C1D1中,E,F,H分别为A1B1,B1C1,CC1的中点.
如图,正方体ABCD-A1B1C1D1中,E,F,H分别为A1B1,B1C1,CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若lna-lnb=a-3b,则a<b<0 | B. | 若lna-lnb=a-3b,则0<a<b | ||
| C. | 若lna-lnb=3b-a,则a>b>0 | D. | 若lna-lnb=3b-a,则0>a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com