
分析 (Ⅰ)化简函数,再求函数f(x)的最小正周期和图象的对称轴方程;
(Ⅱ)利用正弦函数的性质,讨论函数f(x)在区间[-$\frac{π}{12}$,$\frac{π}{2}$]上单调性并求出的值域.
解答 解:(Ⅰ)$f(x)=cos(2x-\frac{π}{3})+$$2sin(x-\frac{π}{4})sin(x+\frac{π}{4})$=$\frac{1}{2}cos2x+\frac{{\sqrt{3}}}{2}sin2x+$(sinx-cosx)(sinx+cosx)=$\frac{1}{2}cos2x+\frac{{\sqrt{3}}}{2}sin2x+{sin^2}x-{cos^2}x$=$\frac{1}{2}cos2x+\frac{{\sqrt{3}}}{2}sin2x-cos2x$=$sin(2x-\frac{π}{6})$.
∴周期$T=\frac{2π}{2}=π$.
由$2x-\frac{π}{6}=kπ+\frac{π}{2}(k∈Z)$,得$x=\frac{kπ}{2}+\frac{π}{3}(k∈Z)$.
∴函数图象的对称轴方程为$x=\frac{kπ}{2}+\frac{π}{3}(k∈Z)$.
(Ⅱ)∵$x∈[-\frac{π}{12},\frac{π}{2}]$,∴$2x-\frac{π}{6}∈[-\frac{π}{3},\frac{5π}{6}]$.
$f(x)=sin(2x-\frac{π}{6})$在区间$[-\frac{π}{12},\frac{π}{3}]$上单调递增,在区间$[\frac{π}{3},\frac{π}{2}]$上单调递减,
当$x=\frac{π}{3}$时,f(x)取最大值1.
∵$f(-\frac{π}{12})=-\frac{{\sqrt{3}}}{2}<f(\frac{π}{2})=\frac{1}{2}$.
∴$x=-\frac{π}{12}$,$f{(x)_{max}}=-\frac{{\sqrt{3}}}{2}$.
所以值域为$[-\frac{{\sqrt{3}}}{2},1]$.
点评 本题考查三角函数的图象与性质,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
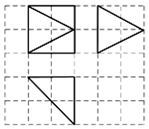 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,几何体的表面积为( )| A. | 4+2($\sqrt{2}$+$\sqrt{3}$) | B. | 6+2($\sqrt{2}$+$\sqrt{5}$) | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 设函数y=f(x)在区间[0,1]上的图象是连续不断的一条曲线,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算由曲线y=f(x)及直线x=0,x=1,y=0所围成部分的面积S,先生产两组(每组N个)区间[0,1]上均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得S的近似值为$\frac{{N}_{1}}{N}$.
设函数y=f(x)在区间[0,1]上的图象是连续不断的一条曲线,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算由曲线y=f(x)及直线x=0,x=1,y=0所围成部分的面积S,先生产两组(每组N个)区间[0,1]上均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得S的近似值为$\frac{{N}_{1}}{N}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=8$\sqrt{5}$x | B. | y2=4$\sqrt{5}$x | C. | y2=2$\sqrt{5}$x | D. | y2=$\sqrt{5}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com