
已知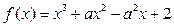 .
.
(1)若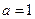 ,求曲线
,求曲线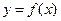 在点
在点 处的切线方程;
处的切线方程;
(2)若 求函数
求函数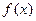 的单调区间;
的单调区间;
(3)若不等式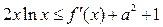 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源:2014高考名师推荐数学理科余弦定理(解析版) 题型:选择题
已知A,B,C为△ABC的三个内角,其所对的边分别为a,b,c,若A= ,a=2
,a=2 ,b+c=4,则△ABC的面积为( )
,b+c=4,则△ABC的面积为( )
A.2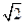
B.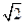
C.3
D.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科三角函数图象变换(解析版) 题型:选择题
函数f(x)=2sin( x+
x+ )(
)( >0, -
>0, - <
< <
< )的部分图象如图所示,则
)的部分图象如图所示,则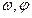 的值分别是( )
的值分别是( )

A.2,- B.2,
B.2,  C.4, -
C.4, - D.4,
D.4, 
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科频率分布直方图、茎叶图(解析版) 题型:选择题
某校开展“爱我海西、爱我家乡”摄影比赛,9位评委为参赛作品A给出的分数如下图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91.复核员在复核时,发现有一个数字(茎叶图中的x)无法看清.若记分员计算无误,则数字x应该是( ).

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ,
, 是正三角形,平面
是正三角形,平面 平面
平面 .
.
(1)求证: ;
;
(2)求三棱锥 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
如图, ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, ,
, 分别是
分别是 ,
, 的中点,
的中点, .
.
(1)证明: ;
;
(2)证明: ;
;
(3)假设这是个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果鱼游到四棱锥 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.

查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科选择题专项训练(解析版) 题型:选择题
已知m,n是两条不同直线,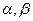 是两个不同平面,以下命题正确的是( )
是两个不同平面,以下命题正确的是( )
A.若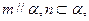 则
则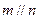
B.若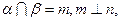 则
则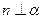
C.若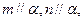 则
则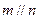
D.若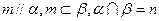 则
则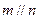
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题后三题(解析版) 题型:解答题
已知曲线 满足下列条件:
满足下列条件:
①过原点;②在 处导数为-1;③在
处导数为-1;③在 处切线方程为
处切线方程为 .
.
(1) 求实数 的值;
的值;
(2)求函数 的极值.
的极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com