
 已知函数$f(x)=sin(-\frac{xπ}{2}+\frac{π}{3})$.
已知函数$f(x)=sin(-\frac{xπ}{2}+\frac{π}{3})$.分析 (1)分别令$\frac{xπ}{2}$+$\frac{2π}{3}$=0,$\frac{π}{2}$,π,$\frac{3π}{2}$,2π,得到相应的x的值及y的值,再描点即可;
(2)令2kπ-$\frac{π}{2}$≤$\frac{xπ}{2}$+$\frac{2π}{3}$≤2kπ+$\frac{π}{2}$ (k∈Z),可解得该函数的增区间.
解答 解:(1)$f(x)=sin(-\frac{xπ}{2}+\frac{π}{3})=-sin(\frac{xπ}{2}-\frac{π}{3})=sin(\frac{xπ}{2}+\frac{2π}{3})$,
列表如下:
| x | $-\frac{4}{3}$ | $-\frac{1}{3}$ | $\frac{2}{3}$ | $\frac{5}{3}$ | $\frac{8}{3}$ |
| y | 0 | 1 | 0 | -1 | 0 |
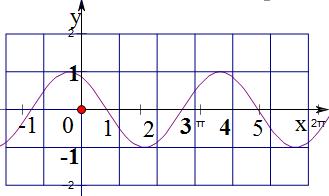 …(6分)
…(6分)点评 本题考查五点法作函数y=Asin(ωx+φ)的图象,着重考查正弦函数的单调性,属于基础题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:填空题
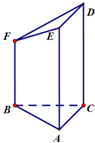 几何体ABCDEF如图所示,其中AC⊥AB,AC=3,AB=4,AE、CD、BF均垂直于面ABC,且AE=CD=5,BF=3,则这个几何体的体积为26.
几何体ABCDEF如图所示,其中AC⊥AB,AC=3,AB=4,AE、CD、BF均垂直于面ABC,且AE=CD=5,BF=3,则这个几何体的体积为26.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
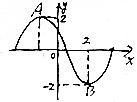 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示,其中A,B两点间距离为5,则f(x)的递增区间是[6k-$\frac{7}{6}$,6k$\frac{1}{6}$](k∈Z).
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示,其中A,B两点间距离为5,则f(x)的递增区间是[6k-$\frac{7}{6}$,6k$\frac{1}{6}$](k∈Z).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
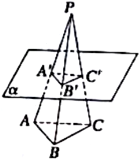 已知P为△ABC所在平面外一点,平面α∥平面ABC,且α交线段PA,PB,PC于点A′,B′,C′,若PA′:AA′=2:3,则S△A′B′C′:S△ABC=( )
已知P为△ABC所在平面外一点,平面α∥平面ABC,且α交线段PA,PB,PC于点A′,B′,C′,若PA′:AA′=2:3,则S△A′B′C′:S△ABC=( )| A. | 2:3 | B. | 2:5 | C. | 4:9 | D. | 4:25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
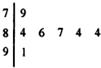 在某校举办的“激扬青春,勇担责任”演讲比赛中,有七位评委选手打分,若选手甲所得分数用茎叶图表示如图,则选手甲所得分数的中位数为( )
在某校举办的“激扬青春,勇担责任”演讲比赛中,有七位评委选手打分,若选手甲所得分数用茎叶图表示如图,则选手甲所得分数的中位数为( )| A. | 87 | B. | 86 | C. | 85 | D. | 84 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
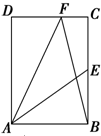
| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com