
分析 令f(λ)=$|\begin{array}{l}{λ-1}&{-2}\\{1}&{λ-4}\end{array}|$=λ2-5λ+6=0,解得λ=2或3.分别对应的一个特征向量为$[\begin{array}{l}{2}\\{1}\end{array}]$;$[\begin{array}{l}{1}\\{1}\end{array}]$.设$[\begin{array}{l}{5}\\{3}\end{array}]$=m$[\begin{array}{l}{2}\\{1}\end{array}]$++n$[\begin{array}{l}{1}\\{1}\end{array}]$.解得m,n,即可得出.
解答 解:∵f(λ)=$|\begin{array}{l}{λ-1}&{-2}\\{1}&{λ-4}\end{array}|$=λ2-5λ+6,由f(λ)=0,解得λ=2或3.
当λ=2时,对应的一个特征向量为α1=$[\begin{array}{l}{2}\\{1}\end{array}]$;当λ=3时,对应的一个特征向量为α2=$[\begin{array}{l}{1}\\{1}\end{array}]$.
设$[\begin{array}{l}{5}\\{3}\end{array}]$=m$[\begin{array}{l}{2}\\{1}\end{array}]$++n$[\begin{array}{l}{1}\\{1}\end{array}]$.解得$\left\{\begin{array}{l}{m=2}\\{n=1}\end{array}\right.$.
∴A5$\overrightarrow{a}$=2×25$[\begin{array}{l}{2}\\{1}\end{array}]$+1×35$[\begin{array}{l}{1}\\{1}\end{array}]$=$[\begin{array}{l}{371}\\{307}\end{array}]$.
点评 本题考查了矩阵与变换、特征向量,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
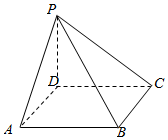 已知线段PD垂直于正方形ABCD所在平面,D为垂足,PD=3,AB=4,连接PA、PB、PC.
已知线段PD垂直于正方形ABCD所在平面,D为垂足,PD=3,AB=4,连接PA、PB、PC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (0,3] | C. | (0,3) | D. | (-1,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com