Question

2．如图，公路AM、AN围成的是一块顶角为α的角形耕地，其中tanα=-2．在该块土地中P处有一小型建筑，经测量，它到公路AM，AN的距离分别为3km，$\sqrt{5}$km．现要过点P修建一条直线公路BC，将三条公路围成的区域ABC建成一个工业园．
（1）现有两种方案：
①方案一：以A为原点，AB为x轴，建立平面直角坐标系，
设直线BC的斜率为k，把△ABC的面积S表示为关于k的函数；
②方案二：设AB=x，AC=y，把△ABC的面积S表示为x、y关系式，并说明x、y满足的关系．
（2）任选一种方案，确定B点的位置，使得该工业园区的面积最小？并求最小面积．

Answer 1

分析 方法一、以A为原点，AB为x轴，建立平面直角坐标系．求出直线AN的方程，设点P（x₀，y₀），根据条件求得P的坐标，设出BC的方程，求得B的横坐标和C的纵坐标，求得S=$\frac{1}{2}$?x_B?y_C的解析式，运用导数求得单调区间，可得极小值也为最小值；
方法二、同方法一求得S=$\frac{1}{2}$?x_B?y_C的解析式，运用换元法和对勾函数的单调性，可得最小值；
方法三、过点P作PE⊥AM，PF⊥AN，垂足为E、F，连接PA．设AB=x，AC=y．由S_△ABC=S_△ABP+S_△APC，求得面积的表达式，运用基本不等式可得最小值．

解答 解：（方法一）如图1，以A为原点，AB为x轴，建立平面直角坐标系．
因为tanα=-2，故直线AN的方程是y=-2x．
设点P（x₀，y₀）．因为点P到AM的距离为3，故y₀=3．
由P到直线AN的距离为$\sqrt{5}$，
得$\frac{|2{x}_{0}+{y}_{0}|}{\sqrt{5}}$=$\sqrt{5}$，解得x₀=1或x₀=-4（舍去），
所以点P（1，3）．                               …（4分）
显然直线BC的斜率存在．设直线BC的方程为y-3=k（x-1），k∈（-2，0）．
令y=0得x_B=1-$\frac{3}{k}$．                           …（6分）
由$\left\{\begin{array}{l}y-3=k（x-1）\\ y=-2x\end{array}$解得y_C=$\frac{6-2k}{k+2}$．              …（8分）
设△ABC的面积为S，则S=$\frac{1}{2}$?x_B?y_C=$\frac{-{k}^{2}+6k-9}{{k}^{2}+2k}$=-1+$\frac{8k-9}{{k}^{2}+2k}$．  …（10分）
由S′=$\frac{-2（4k+3）（k-3）}{（{k}^{2}+2k）^{2}}$=0得k=-$\frac{3}{4}$或k=3．
当-2＜k＜-$\frac{3}{4}$时，S′＜0，S单调递减；当-$\frac{3}{4}$＜k＜0时，S′＞0，S单调递增．…（13分）
所以当k=-$\frac{3}{4}$时，即AB=5时，S取极小值，也为最小值15．
答：当AB=5km时，该工业园区的面积最小，最小面积为15km²．…（16分）
（方法二）同方法一：S=$\frac{1}{2}$?x_B?y_C=$\frac{-{k}^{2}+6k-9}{{k}^{2}+2k}$=-1+$\frac{8k-9}{{k}^{2}+2k}$．   …（10分）
令8k-9=t，则t∈（-25，-9），从而k=$\frac{t+9}{8}$．
因此S=-1+$\frac{t}{（\frac{t+9}{8}）^{2}+2•\frac{t+9}{8}}$=-1+$\frac{64t}{{t}^{2}+34t+225}$=-1+$\frac{64}{34+t+\frac{225}{t}}$．…（13分）
因为当t∈（-25，-9）时，t+$\frac{225}{t}$∈（-34，-30]，
当且仅当t=-15时，此时AB=5，34+t+$\frac{225}{t}$的最大值为4．从而S有最小值为15．
答：当AB=5km时，该工业园区的面积最小，最小面积为15km²．…（16分）
（方法三）如图2，过点P作PE⊥AM，PF⊥AN，垂足为E、F，连接PA．设AB=x，AC=y．
因为P到AM，AN的距离分别为3，$\sqrt{5}$，
即PE=3，PF=$\sqrt{5}$．
由S_△ABC=S_△ABP+S_△APC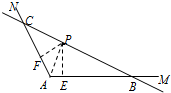
=$\frac{1}{2}$?x?3+$\frac{1}{2}$?y?$\sqrt{5}$=$\frac{1}{2}$（3x+$\sqrt{5}$y）．  ①…（4分）
因为tanα=-2，所以sinα=$\frac{2}{\sqrt{5}}$．
所以S_△ABC=$\frac{1}{2}$?x?y?$\frac{2}{\sqrt{5}}$．  ②…（8分）
由①②可得$\frac{1}{2}$?x?y?$\frac{2}{\sqrt{5}}$=$\frac{1}{2}$（3x+$\sqrt{5}$y）．
即3$\sqrt{5}$x+5y=2xy． ③…（10分）
因为3$\sqrt{5}$x+5y≥2$\sqrt{15\sqrt{5}xy}$，所以 2xy≥2$\sqrt{15\sqrt{5}xy}$．
解得xy≥15$\sqrt{5}$．                          …（13分）
当且仅当3$\sqrt{5}$x=5y取“=”，结合③解得x=5，y=3$\sqrt{5}$．
所以S_△ABC=$\frac{1}{2}$?x?y?$\frac{2}{\sqrt{5}}$有最小值15．
答：当AB=5km时，该工业园区的面积最小，最小面积为15km²．…（16分）

点评 本题考查数学模型法在实际问题中的运用，考查函数最值的求法，注意运用导数、单调性和基本不等式，考查化简整理的运算能力，属于中档题．