
分析 (1)利用等可能事件概率计算公式能求出该卡片上写有数字1的概率.
(2)依题意先用列举法分析所有等可能事件的所有结果的可能,然后利用概率计算公式能求出该事件的概率.
解答 解:(1)∵在7张卡片中共有2张写有数字1,
∴从中任取一张卡片,卡片上写有数字1的概率为$\frac{2}{7}$.
(2)组成的所有的两位数有:
(11),(12),(13),(21),(22),(23),
(31),(32),(33),(41),(42),(43),
共有12个,
这个两位数大于22的有:(23),(31),(32),
(33),(41),(42),(43),共有7个,
∴这个两位数大于22的概率p=$\frac{7}{12}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 如图,公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,$\sqrt{5}$km.现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.
如图,公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,$\sqrt{5}$km.现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
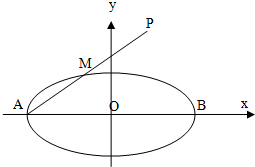 已知椭圆C;$\frac{x^2}{4}+\frac{y^2}{b}$=1(0<b<4)的左右顶点分别为A、B,M为椭圆上的任意一点,A关于M的对称点为P,如图所示,
已知椭圆C;$\frac{x^2}{4}+\frac{y^2}{b}$=1(0<b<4)的左右顶点分别为A、B,M为椭圆上的任意一点,A关于M的对称点为P,如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com