
分析 (1)设f(x)+2x=a(x-1)(x-3),求出函数的解析式,由方程f(x)+6a=0,方程有两个相等的根,求出a,然后求解f(x)的解析式.
(2)利用x1=-3,x2=m是方程f(x)=0的两个根.转化当-1≤x≤0时,f(x)≤0恒成立.推出不等式组求解即可.
解答 解:(1)据题意,设f(x)+2x=a(x-1)(x-3),
f(x)=a(x-1)(x-3)-2x=ax2-(2+4a)x+3a,①
由方程f(x)+6a=0可得ax2-(2+4a)x+9a=0 ②
因为方程②有两个相等的根,所以△=[-(2+4a)]2-4a•9a=0,
即5a2-4a-1=0,解得a=1或a=-$\frac{1}{5}$(舍去)
将a=1代入①得f(x)的解析式f(x)=x2-6x+3…(6分)
(2)据题意知,x1=-3,x2=m是方程f(x)=0的两个根.
则f(x)=a(x+3)(x-m),
又a>0,
要使得当-1≤x≤0时,f(x)≤0恒成立.
当且仅当$\left\{\begin{array}{l}{f(-1)≤0}\\{f(0)≤0}\end{array}\right.$,可得$\left\{\begin{array}{l}{2m≥-2}\\{-3m≤0}\end{array}\right.$,
∴m≥0. …(12分)
点评 本题考查二次函数的简单性质以及函数恒成立的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
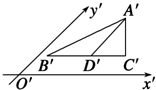 如图所示的是水平放置的三角形直观图,D′是△A′B′C′中B′C′边上的一点,且D′离C′比D′离B′近,又A′D′∥y′轴,那么原△ABC的AB、AD、AC三条线段中 ( )
如图所示的是水平放置的三角形直观图,D′是△A′B′C′中B′C′边上的一点,且D′离C′比D′离B′近,又A′D′∥y′轴,那么原△ABC的AB、AD、AC三条线段中 ( )| A. | 最长的是AB,最短的是AC | B. | 最长的是AC,最短的是AB | ||
| C. | 最长的是AB,最短的是AD | D. | 最长的是AD,最短的是AC |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题:?x∈R,使x3+sinx+2<0的否定为:?x∈R,均有x3+sinx+2<0 | |
| B. | 命题:若x2=1,则x=1或x=-1的逆否命题为:若x≠1或x≠-1,则x2≠1. | |
| C. | 己知n∈N,则幂函数y=x3n-7为偶函数,且在(0,+∞)上单调递减的充要条件为n=1 | |
| D. | 把函数y=sin2x的图象沿x轴向左平移$\frac{π}{2}$个单位,可以得到函数y=cos2x的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com