
分析 (Ⅰ)由抛物线C的方程y2=8x,得p=4,即可求抛物线C的准线方程;
(Ⅱ)直线l方程与抛物线C的方程联立,分类讨论求实数k的取值范围;
(Ⅲ)若线段AB中点的横坐标为2,求出k,利用弦长公式求AB的长度.
解答 解:(Ⅰ)由抛物线C的方程y2=8x,得p=4,
所以抛物线C的准线方程为x=-2-------------------(3分)
(Ⅱ)直线l方程与抛物线C的方程联立,得方程组$\left\{\begin{array}{l}y=kx-2\\{y^2}=8x\end{array}\right.$-------------------(1分)
消y,整理得k2x2-(4k+8)x+4=0,①-------------------(2分)
由直线l与抛物线C交于不同的两点A,B,则有△=(4k+8)2-16k2>0-------------------(1分)
解得k>-1
当k=0时,直线l与抛物线C只有一个交点,所以k的取值范围是k>-1且k≠0------------------(1分)
(Ⅲ)若线段AB中点的横坐标为2,设A(x1,y1),B(x2,y2),
由(Ⅱ)中的①式得${x_1}+{x_2}=\frac{4k+8}{k^2}=4$,-------------------(2分)
解得k=2或k=-1(舍)-------------------(1分)
$|AB|=\sqrt{(1+{k^2})[{{({x_1}+{x_2})}^2}-4{x_1}{x_2}]}=2\sqrt{15}$-------------------(2分)
点评 本题考查抛物线的方程与性质,考查直线与抛物线的位置关系,考查弦长的计算,属于中档题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄段分组 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 频数 | 300 | 320 | 160 | 160 | 40 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
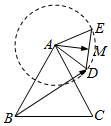 如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )
如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{4}$+$\sqrt{3}$ | C. | $\frac{3+\sqrt{3}}{4}$ | D. | $\frac{3}{4}$+2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com