
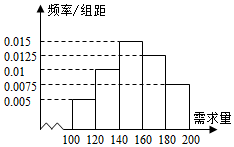
 大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小李给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.
大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小李给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.分析 (1)当160≤X≤200时,Y=500×160=80000,当100≤X<160时,Y=500X-(160-X)×300=800X-48000,由此能将将Y表示为X的函数.
(2)由利润Y不少于64000元,得800X-48000≥64000,由此利用频率分布直方图能估计利润Y不少于64000元的概率.
(3)由频率分布直方图能求出Y的数学期望.
解答 解:(1)∵在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.
小李给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,
Y(单位:元)表示今年葡萄销售的利润,
∴当160≤X≤200时,Y=500×160=80000,
当100≤X<160时,
Y=500X-(160-X)×300=800X-48000,
∴Y=$\left\{\begin{array}{l}{80000,160≤X≤200}\\{800X-48000,100≤X<160}\end{array}\right.$.
(2)∵利润Y不少于64000元,
∴800X-48000≥64000,
∴X≥140.
由频率分布直方图得X≥140的频率为:(0.015+0.0125+0.0075)×20=0.7,
∴根据直方图估计利润Y不少于64000元的概率为0.7.
(3)EY=110×0.005×20+130×0.01×20+150×0.015×20+170×0.0125×20+190×0.0075×20=153.
∴Y的数学期望为153.
点评 本题考查函数表达式的求法,考查概率的求法,考查随时机变量的数学期望的求法,是中档题,解题时要认真审题,注意频率分布直方图的合理运用.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
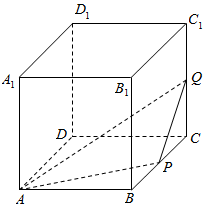 正方体ABCD-A1B1C1D1的棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是②.(写出所有正确命题的编号)
正方体ABCD-A1B1C1D1的棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是②.(写出所有正确命题的编号)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
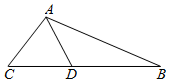 如图,在△ABC中,∠BAC=120°,AB=2,AC=1,D是BC边上的一点(包括端点),若$\overrightarrow{AD}$•$\overrightarrow{BC}$∈[m,n],则$\frac{n}{m-n}$的值为$-\frac{2}{7}$.
如图,在△ABC中,∠BAC=120°,AB=2,AC=1,D是BC边上的一点(包括端点),若$\overrightarrow{AD}$•$\overrightarrow{BC}$∈[m,n],则$\frac{n}{m-n}$的值为$-\frac{2}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为贯彻落实教育部6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,培养拼搏意识和团队精神,普及足球知识和技能,市教体局决定举行春季校园足球联赛.为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,记录入如表:(设ξ为随机变量)
为贯彻落实教育部6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,培养拼搏意识和团队精神,普及足球知识和技能,市教体局决定举行春季校园足球联赛.为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,记录入如表:(设ξ为随机变量)| 身高(cm) | 168 | 174 | 175 | 176 | 178 | 182 | 185 | 188 |
| 人数 | 1 | 2 | 4 | 3 | 5 | 1 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com