
 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\sqrt{3})$ | B. | $(1,\sqrt{3})$ | C. | $(\sqrt{3},+∞)$ | D. | (0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
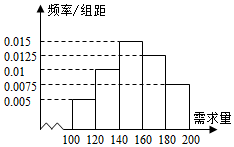 大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小李给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.
大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小李给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 26 | B. | 30 | C. | 36 | D. | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com