
分析 利用双曲线的渐近线的定义及其求法即可判断出结论.
解答 解:双曲线C的标准方程为$\frac{x^2}{16}$-$\frac{y^2}{9}$=1”可得:“双曲线C的渐近线方程为y=±$\frac{3}{4}$x”,反之不成立,例如双曲线$\frac{{x}^{2}}{64}-\frac{{y}^{2}}{36}$=1是渐近线方程仍然为y=±$\frac{3}{4}$x.
∴,“双曲线C的标准方程为$\frac{x^2}{16}$-$\frac{y^2}{9}$=1”是“双曲线C的渐近线方程为y=±$\frac{3}{4}$x”成立的充分非必要条件.
故答案为:充分非必要.
点评 本题考查了双曲线的标准方程及其性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{2\sqrt{3}}}{3}$ | C. | $-\frac{{9\sqrt{3}}}{2}$ | D. | $-\frac{{2\sqrt{3}}}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x≤1} | B. | {x|1<x<2} | C. | {x|0<x<1} | D. | {x|1≤x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
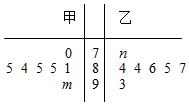 如图是七位评委为甲,乙两名参赛歌手打出的分数的茎叶图(其中m,n为数字0~9中的一个),则甲歌手得分的众数和乙歌手得分的中位数分别为a和b,则一定有( )
如图是七位评委为甲,乙两名参赛歌手打出的分数的茎叶图(其中m,n为数字0~9中的一个),则甲歌手得分的众数和乙歌手得分的中位数分别为a和b,则一定有( )| A. | a>b | B. | a<b | ||
| C. | a=b | D. | a,b的大小与m,n的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2×(31008-1) | B. | 2×31008 | C. | $\frac{{{3^{2016}}-1}}{2}$ | D. | $\frac{{{3^{2016}}+1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com