
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{2\sqrt{3}}}{3}$ | C. | $-\frac{{9\sqrt{3}}}{2}$ | D. | $-\frac{{2\sqrt{3}}}{27}$ |
分析 求得双曲线的渐近线方程,将直线y=1-x联立,求得交点A,B的坐标,可得中点坐标,由直线的斜率公式计算即可得到所求值.
解答 解:双曲线ax2+by2=1(a>0,b<0)的渐近线方程为
y=±$\sqrt{\frac{a}{-b}}$x,
把y=1-x代入y=±$\sqrt{\frac{a}{-b}}$x,
可得A($\frac{1}{1+\sqrt{\frac{a}{-b}}}$,$\frac{\sqrt{\frac{a}{-b}}}{1+\sqrt{\frac{a}{-b}}}$),B($\frac{1}{1-\sqrt{\frac{a}{-b}}}$,$\frac{-\sqrt{\frac{a}{-b}}}{1-\sqrt{\frac{a}{-b}}}$),
可得AB的中点M为($\frac{1}{1+\frac{a}{b}}$,$\frac{\frac{a}{b}}{1+\frac{a}{b}}$)
由过原点和线段AB中点的直线的斜率为$-\frac{{\sqrt{3}}}{2}$,
即有kOM=$\frac{{y}_{M}}{{x}_{M}}$=$\frac{a}{b}$=$-\frac{{\sqrt{3}}}{2}$,
故选:A.
点评 本题考查直线的斜率的求法,注意运用联立直线方程求交点,运用中点坐标公式,考查运算能力,属于中档题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
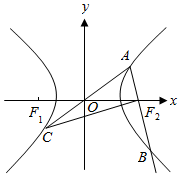 如图,点F1、F2为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左右焦点,点A、B、C分别为双曲线上三个不同的点,且AC经过坐标原点O,并满足$\overrightarrow{A{F_2}}=\frac{1}{2}\overrightarrow{{F_2}B}$,$\overrightarrow{AB}•\overrightarrow{C{F_2}}=0$,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.
如图,点F1、F2为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左右焦点,点A、B、C分别为双曲线上三个不同的点,且AC经过坐标原点O,并满足$\overrightarrow{A{F_2}}=\frac{1}{2}\overrightarrow{{F_2}B}$,$\overrightarrow{AB}•\overrightarrow{C{F_2}}=0$,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{5}-\frac{{y}^{2}}{20}=1$ | B. | $\frac{{x}^{2}}{20}-\frac{{y}^{2}}{5}=1$ | ||
| C. | $\frac{3{x}^{2}}{25}-\frac{3{y}^{2}}{100}=1$ | D. | $\frac{3{x}^{2}}{100}-\frac{3{y}^{2}}{25}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com