
���� ��I������ͬ�����Ǻ����Ĺ�ϵФ�����ȵó���ͨ���̣�
��II���������ߵĶԳ��Կ�֪���߽��������Ľ�ƽ�����ϣ������������ó������ε������
��� �⣺��I������C1����ͨ����Ϊ$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{3}=1$��
��II������C2����ͨ����Ϊx2+y2=r2��
������C1��C2�Ľ����γ�һ�����Σ�
�������ߵĽ���������ֱ��y=��x�ϣ�
����������$\left\{\begin{array}{l}{y=x}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{3}=1}\end{array}\right.$�����x=y=$��\frac{3}{2}$��
���������ڵ�һ�����ڵĽ�������Ϊ��$\frac{3}{2}$��$\frac{3}{2}$����
�����߽��㹹�ɵ����������ΪS=4����$\frac{3}{2}$��2=9��
���� ���⿼���˲�����������ͨ���̵�ת�������ߵĽ����������⣬���ڻ����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1 | B�� | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | C�� | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 | D�� | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{12}$=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{{\sqrt{3}}}{2}$ | B�� | $-\frac{{2\sqrt{3}}}{3}$ | C�� | $-\frac{{9\sqrt{3}}}{2}$ | D�� | $-\frac{{2\sqrt{3}}}{27}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�10] | B�� | [5��10] | C�� | [8��+�ޣ� | D�� | [8��10] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
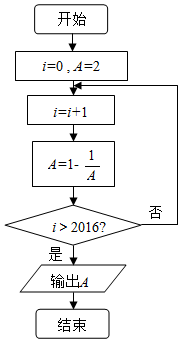
| A�� | -2 | B�� | $\frac{1}{2}$ | C�� | -1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
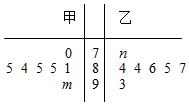 ��ͼ����λ��ίΪ�ף��������������ִ���ķ����ľ�Ҷͼ������m��nΪ����0��9�е�һ����������ֵ÷ֵ��������Ҹ��ֵ÷ֵ���λ���ֱ�Ϊa��b����һ���У�������
��ͼ����λ��ίΪ�ף��������������ִ���ķ����ľ�Ҷͼ������m��nΪ����0��9�е�һ����������ֵ÷ֵ��������Ҹ��ֵ÷ֵ���λ���ֱ�Ϊa��b����һ���У�������| A�� | a��b | B�� | a��b | ||
| C�� | a=b | D�� | a��b�Ĵ�С��m��n��ֵ�й� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com