
分析 (1)设圆P的方程是x2+y2+Dx+Ey+F=0,则由已知得$\left\{\begin{array}{l}{1^2}+{0^2}+D+0+F=0\\{4^2}+{0^2}+4D+0+F=0\\{6^2}+{(-2)^2}+6D-2E+F=0\end{array}\right.$,求出D,E,F,即可求圆P的方程;
(2)若圆心P的纵坐标为 2,求出圆心与半径,即可求圆P的方程.
解答 解:(1)设圆P的方程是x2+y2+Dx+Ey+F=0,则由已知得$\left\{\begin{array}{l}{1^2}+{0^2}+D+0+F=0\\{4^2}+{0^2}+4D+0+F=0\\{6^2}+{(-2)^2}+6D-2E+F=0\end{array}\right.$,解得$\left\{\begin{array}{l}D=-5\\ E=7\\ F=4\end{array}\right.$.
故圆P的方程为x2+y2-5x+7y+4=0.
(2)由圆的对称性可知,圆心P的横坐标为$\frac{1+4}{2}=\frac{5}{2}$,故圆心$P(\frac{5}{2},2)$,
故圆P的半径$r=|AP|=\sqrt{{{(1-\frac{5}{2})}^2}+{{(0-2)}^2}}=\frac{5}{2}$,
故圆P的标准方程为${(x-\frac{5}{2})^2}+{(y-2)^2}=\frac{25}{4}$.
点评 本题考查圆的方程,考查待定系数法的运用,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
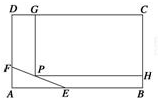 如图所示,为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形ABCD处规划一块长方形地面HPGC,建造住宅小区公园,但不能越过文物保护区三角形AEF的边线EF.已知AB=CD=200m,BC=AD=160m,AF=40m,AE=60m,问如何设计才能使公园占地面积最大,求出最大面积.
如图所示,为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形ABCD处规划一块长方形地面HPGC,建造住宅小区公园,但不能越过文物保护区三角形AEF的边线EF.已知AB=CD=200m,BC=AD=160m,AF=40m,AE=60m,问如何设计才能使公园占地面积最大,求出最大面积.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=1,y=x0 | B. | y=$\sqrt{x-1}$•$\sqrt{x+1}$,y=$\sqrt{{x}^{2}-1}$ | ||
| C. | y=x,y=$\root{3}{{x}^{3}}$ | D. | y=|x|,t=($\sqrt{x}$)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在三棱锥P-ABC中,底面ABC为直角三角形,AB=BC,PA⊥平面ABC.
在三棱锥P-ABC中,底面ABC为直角三角形,AB=BC,PA⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com