
| A. | 2<m≤3 | B. | $\frac{9}{4}<m≤\frac{25}{9}$ | C. | m$>\frac{25}{9}$ | D. | m$≤\frac{9}{4}$ |
分析 根据题意可以先得到0<m<4,从而解方程f(x)=0可得到$x=\frac{1}{2±\sqrt{m}}$,从而f(x)<0的解为$(\frac{1}{2+\sqrt{m}},\frac{1}{2-\sqrt{m}})$,容易得出$\frac{1}{4}<\frac{1}{2+\sqrt{m}}<\frac{1}{2}$,这样根据条件a为正整数,满足f(a)<0的a的个数有且仅有两个,从而得出$2<\frac{1}{2-\sqrt{m}}≤3$,这样解该不等式便可得出实数m的取值范围.
解答 解:若m=4,则f(x)=-4x+1,则满足f(a)<0的a有无数个,不满足条件,即m≠4,依题意m<4;
根据题意,方程f(x)=0有两个不同实数根;
∴△=16-4(4-m)=4m>0;
即0<m<4;
解(4-m)x2-4x+1=0得,$x=\frac{1}{2±\sqrt{m}}$;
∴f(x)<0的解为$(\frac{1}{2+\sqrt{m}},\frac{1}{2-\sqrt{m}})$;
∵0<m<4;
∴$2<2+\sqrt{m}<4$;
∴$\frac{1}{4}<\frac{1}{2+\sqrt{m}}<\frac{1}{2}$;
∵满足f(a)<0的a的个数有且仅有两个,且a为正整数;
∴$2<\frac{1}{2-\sqrt{m}}≤3$;
解得$\frac{9}{4}<m≤\frac{25}{9}$.
故选B.
点评 考查二次函数的图象,以及一元二次方程的实数根的个数和判别式△取值的关系,一元二次方程的求根公式,以及不等式的性质,分式不等式的解法.


科目:高中数学 来源: 题型:选择题
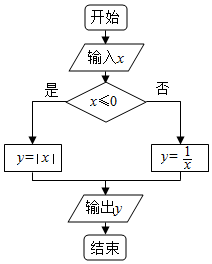 如图给出了一个程序框图,其作用是输入实数x的值,输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值有( )
如图给出了一个程序框图,其作用是输入实数x的值,输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
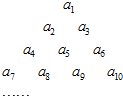 设数列{an}按三角形进行排列,如图,第一层一个数a1,第二层两个数a2和a3,第三层三个数a4,a5和a6,以此类推,且每个数字等于下一层的左右两个数字之和,如a1=a2+a3,a2=a4+a5,a3=a5+a6,….
设数列{an}按三角形进行排列,如图,第一层一个数a1,第二层两个数a2和a3,第三层三个数a4,a5和a6,以此类推,且每个数字等于下一层的左右两个数字之和,如a1=a2+a3,a2=a4+a5,a3=a5+a6,….查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | -3 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}i$ | B. | $\frac{1}{2}i$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com