
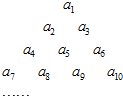 设数列{an}按三角形进行排列,如图,第一层一个数a1,第二层两个数a2和a3,第三层三个数a4,a5和a6,以此类推,且每个数字等于下一层的左右两个数字之和,如a1=a2+a3,a2=a4+a5,a3=a5+a6,….
设数列{an}按三角形进行排列,如图,第一层一个数a1,第二层两个数a2和a3,第三层三个数a4,a5和a6,以此类推,且每个数字等于下一层的左右两个数字之和,如a1=a2+a3,a2=a4+a5,a3=a5+a6,….分析 (1)若第四层四个数为0或1,则a1=a7+3a8+3a9+a10,由a1为奇数,进而得到答案;
(2)若第十一层十一个数为0或1,a1为5的倍数,则若a1为5的倍数,则a56,a66均为0,a57,a58,a65任意,进而得到答案.
解答 解:(1)若第四层四个数为0或1,则a1=a7+3a8+3a9+a10,
则a7,a8,a9,a10中有一个1,或有三个1,
若a7,a8,a9,a10中有一个1,则有4种情况;
若a7,a8,a9,a10中有三个1,则有4种情况;
共8种情况;
(2)根据(1)中结论,若第十一层十一个数为0或1,
则a1=a56+10(a57+a58+…+a65)+a66,
若a1为5的倍数,则a56,a66均为0,
a57,a58,a65任意,
则第十一层十一个数共有29=512种不同取法.
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>-10 | B. | m<-10 | C. | m>-8 | D. | m<-8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{15}}}{3}$ | C. | $-\frac{{\sqrt{15}}}{5}$ | D. | $-\frac{{\sqrt{15}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2<m≤3 | B. | $\frac{9}{4}<m≤\frac{25}{9}$ | C. | m$>\frac{25}{9}$ | D. | m$≤\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com