
���� ��1��������Բ�Ķ���ɵ�2a=6����a=3�����ɹ��ɶ����ɵ�c������a��b��c�Ĺ�ϵ���ɵ�b�����ɵõ���Բ���̣�
��2����A��B������ֱ�Ϊ��x1��y1������x2��y2�������AB�ķ��̣�������Բ���̣���Τ�ﶨ�����е����깫ʽ���ⷽ�̿ɵ�k�������õ�ֱ��AB�ķ��̣�
��3��ֱ��TQ��ԲN���У������Բ���ҽ�������ߣ�����б�ʹ�ʽ����ֱ��������б��֮��Ϊ-1�����ɵõ����ۣ�
��� �⣺��1����$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������Ϊ��P����ԲC�ϣ�
����2a=|PF1|+|PF2|=6��
���a=3��
��ֱ�ǡ�PF1F2�У�|F1F2|=$\sqrt{|P{F}_{2}{|}^{2}+|P{F}_{1}{|}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$��
����Բ�İ뽹��c=$\sqrt{5}$��
�Ӷ�b2=a2-c2=9-5=4��
������ԲC�ķ���Ϊ$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1��
��2����A��B������ֱ�Ϊ��x1��y1������x2��y2����
��Բ�ķ���Ϊ��x+2��2+��y-1��2=9������Բ��M������Ϊ��-2��1����
�Ӷ�����ֱ��l�ķ���Ϊy=k��x+2��+1��������ԲC�ķ��̵�
��5+9k2��x2+18��2k2+k��x+36��k2+k-1��=0��
��ΪA��B���ڵ�M�Գƣ�����$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{9��2{k}^{2}+k��}{5+9{k}^{2}}$=-2��
���k=$\frac{10}{9}$��
����ֱ��l�ķ���Ϊy=$\frac{10}{9}$��x+2��+1��
��10x-9y+29=0���������飬�������⣩��
��3��ֱ��TQ��ԲN���У�֤�����£�����Բ�ҽ���ΪF2��$\sqrt{5}$��0��������Ϊx=$\frac{9\sqrt{5}}{5}$��
���T��x0��y0��������x02+y02=9����${k}_{T{F}_{2}}$=$\frac{{y}_{0}}{{x}_{0}-\sqrt{5}}$��kOQ=-$\frac{{x}_{0}-\sqrt{5}}{{y}_{0}}$��
��ֱ��OQ�ķ���Ϊy=-$\frac{{x}_{0}-\sqrt{5}}{{y}_{0}}$x����x=$\frac{9\sqrt{5}}{5}$����y=-$\frac{9\sqrt{5}��{x}_{0}-\sqrt{2}��}{5{y}_{0}}$��
��Q��$\frac{9\sqrt{5}}{5}$��-$\frac{9\sqrt{5}��{x}_{0}-\sqrt{2}��}{5{y}_{0}}$����
����kTQ=$\frac{{y}_{0}+\frac{9\sqrt{5}��{x}_{0}-\sqrt{5}��}{5{y}_{0}}}{{x}_{0}-\frac{9\sqrt{5}}{5}}$=$\frac{5{{y}_{0}}^{2}+9\sqrt{5}��{x}_{0}-\sqrt{5}��}{{y}_{0}��5{x}_{0}-9\sqrt{5}��}$=$\frac{5��9-{{x}_{0}}^{2}��+9\sqrt{5}��{x}_{0}-\sqrt{5}��}{{y}_{0}��5{x}_{0}-9\sqrt{5}��}$=-$\frac{{x}_{0}}{{y}_{0}}$��
��kOT=$\frac{{y}_{0}}{{x}_{0}}$��������kOT•kTQ=-1��
��OT��TQ����ֱ��TQ��ԲN���У�
���� ���⿼����Բ�Ķ��塢���̺����ʣ���Ҫ������Բ�Ķ���ͷ��̵����ã�����ֱ�߷��̣�����Τ�ﶨ�����е����깫ʽ��ͬʱ����ֱ�ߺ�Բ��λ�ù�ϵ���жϣ��������������������е��⣮


 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $1+\frac{ln2}{2}$ | B�� | $1-\frac{ln2}{2}$ | C�� | $2\sqrt{e}-1$ | D�� | $\sqrt{e}-1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
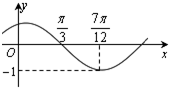 ����f��x��=Acos����x+�գ�������A��0���أ�0��|��|��$\frac{��}{2}$����ͼ����ͼ��ʾ���Ѻ���f��x����ͼ������ƽ��$\frac{��}{6}$����λ��������ƽ��1����λ���õ�����y=g��x����ͼ��
����f��x��=Acos����x+�գ�������A��0���أ�0��|��|��$\frac{��}{2}$����ͼ����ͼ��ʾ���Ѻ���f��x����ͼ������ƽ��$\frac{��}{6}$����λ��������ƽ��1����λ���õ�����y=g��x����ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
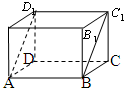 ��ͼ���ڳ�����ABCD-A1B1C1D1�У�AB=5��BC=4��AA1=3���ظó�����Խ���ABC1D1����س������֣�����������ƴ��һ���µ�����������ô�������������������ֵΪ114��
��ͼ���ڳ�����ABCD-A1B1C1D1�У�AB=5��BC=4��AA1=3���ظó�����Խ���ABC1D1����س������֣�����������ƴ��һ���µ�����������ô�������������������ֵΪ114���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
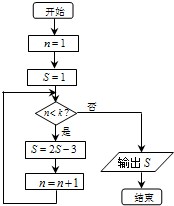
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{1��1+\frac{{\sqrt{2}}}{2}}��$ | B�� | $��{1+\frac{{\sqrt{2}}}{2}��+��}��$ | C�� | $��{1��1+\sqrt{2}}��$ | D�� | $��{1+\sqrt{2}��+��}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{127}{64}$ | B�� | $\frac{511}{256}$ | C�� | $\frac{1023}{512}$ | D�� | $\frac{511}{512}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com