
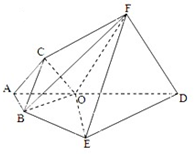
 如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODF,△ODE都是正三角形.
如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODF,△ODE都是正三角形.
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
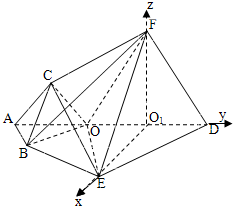
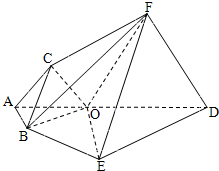 (1)证明:设G是线段DA与EB延长线的交点.
(1)证明:设G是线段DA与EB延长线的交点.
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| OC |
| 1 |
| 2 |
| ||
| 2 |
| EF |
| 3 |
| 3 |
| OC |
| EF |
| ||||||
1×
|
| ||
1×
|
| ||
| 4 |
| ||
| 4 |
| CE |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| CF |
| 3 |
| 2 |
| ||
| 2 |
| n1 |
|
| n1 |
| 3 |
| 3 |
| n2 |
| 3 |
| n1 |
| n2 |
| ||||||
|
| ||
| 35 |
| ||
| 35 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 已知圆C:(x-1)2+(y-1)2=2经过椭圆Γ:
已知圆C:(x-1)2+(y-1)2=2经过椭圆Γ:| x2 |
| a2 |
| y2 |
| b2 |
| OM |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知⊙O的直径AB=3,点C为⊙O上异于A,B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.
如图,已知⊙O的直径AB=3,点C为⊙O上异于A,B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
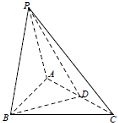 如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.
如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.查看答案和解析>>
科目:高中数学 来源: 题型:
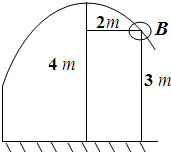 有一次姚明投篮时,测得投篮的轨迹是抛物线,如图所示,抛物线最高点离地面距离4m,篮筐B高为3m,篮筐中心离最高点的水平距离为2m,求投中时抛物线的方程?
有一次姚明投篮时,测得投篮的轨迹是抛物线,如图所示,抛物线最高点离地面距离4m,篮筐B高为3m,篮筐中心离最高点的水平距离为2m,求投中时抛物线的方程?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com