
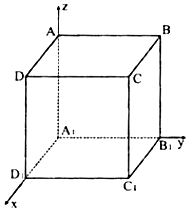
 如图建立空间直角坐标系,已知正方体的棱长为2.
如图建立空间直角坐标系,已知正方体的棱长为2.分析 (1)由已知利用坐标意义即可得出.
(2)解法一:利用两点之间的距离公式即可得出.
解法二:利用勾股定理即可得出.
解答 解:(1)正方体各顶点的坐标如下:A1(0,0,0),B1(0,2,0),C1(2,2,0),D1(2,0,0),A(0,0,2),B(0,2,2),C(2,2,2),D(2,0,2)
(2)解法一:$|{{A_1}C}|=\sqrt{{2^2}+{2^2}+{2^2}}=2\sqrt{3}$.
解法二:∵$|{{A_1}{C_1}}|=2\sqrt{2},|{A{A_1}}|=2$,
在Rt△AA1C1中,${|{A{C_1}}|^2}={|{A{A_1}}|^2}+{|{{A_1}{C_1}}|^2}$,
∴${|{A{C_1}}|^2}={2^2}+{(2\sqrt{2})^2}=12$,∴$|{A{C_1}}|=2\sqrt{3}$,∴$|{{A_1}C}|=2\sqrt{3}$.
点评 本题考查了空间向量坐标、两点之间的距离公式、勾股定理、正方体的性质,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 6$\sqrt{2}$+4$\sqrt{5}$ | B. | 6$\sqrt{2}$+2$\sqrt{5}$ | C. | 3$\sqrt{2}$+4$\sqrt{5}$ | D. | 3$\sqrt{2}$+2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
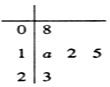 如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )
如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )| A. | $\frac{68}{5}$ | B. | $\frac{69}{5}$ | C. | 14 | D. | $\frac{71}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 92,4 | B. | 93,5 | C. | 93,4 | D. | 92,$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com