
(2014•郴州三模)设集合A⊆R,如果x0∈R满足:对任意a>0,都存在x∈A,使得0<|x﹣x0|<a,那么称x0为集合A的一个聚点.则在下列集合中:
(1)Z+∪Z﹣;
(2)R+∪R﹣;
(3){x|x= ,n∈N*};
,n∈N*};
(4){x|x=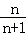 ,n∈N*}.
,n∈N*}.
其中以0为聚点的集合有( )
A.1个 B.2个 C.3个 D.4个
B
【解析】
试题分析:根据集合聚点的新定义,我们逐一分析四个集合中元素的性质,并判断是否满足集合聚点的定义,进而得到答案.
【解析】
(1)对于某个a<1,比如a=0.5,此时对任意的x∈Z+∪Z﹣,都有|x﹣0|=0或者|x﹣0|≥1,也就是说不可能0<|x﹣0|<0.5,从而0不是Z+∪Z﹣的聚点;
(2)集合{x|x∈R,x≠0},对任意的a,都存在x=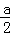 (实际上任意比a小得数都可以),使得0<|x|=
(实际上任意比a小得数都可以),使得0<|x|=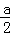 <a,
<a,
∴0是集合{x|x∈R,x≠0}的聚点;
(3)集合{x|x= ,n∈N*}中的元素是极限为0的数列,对于任意的a>0,存在n>
,n∈N*}中的元素是极限为0的数列,对于任意的a>0,存在n> ,使0<|x|=
,使0<|x|= <a,
<a,
∴0是集合 {x|x= ,n∈N*}的聚点;
,n∈N*}的聚点;
(4)中,集合{x|x=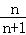 ,n∈N*}中的元素是极限为1的数列,除了第一项0之外,其余的都至少比0大
,n∈N*}中的元素是极限为1的数列,除了第一项0之外,其余的都至少比0大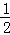 ,
,
∴在a<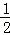 的时候,不存在满足得0<|x|<a的x,
的时候,不存在满足得0<|x|<a的x,
∴0不是集合{x|x=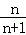 ,n∈N*}的聚点;
,n∈N*}的聚点;
故选:B


科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:填空题
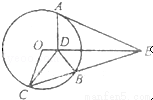
(2014•南开区二模)如图,AE是圆O的切线,A是切点,AD与OE垂直,垂足是D.割线EC交圆D于B,C,且∠BDC=62°,∠DBE=108°,则∠OEC= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷(解析版) 题型:选择题
如图,⊙O是△ABC的内切圆,切点分别是D、E、F,已知∠A=100°,∠C=30°,则∠DFE的度数是( )

A.55° B.60° C.65° D.70°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷(解析版) 题型:选择题
下列表述正确的是( )
①归纳推理是由特殊到一般的推理;
②演绎推理是由一般到特殊的推理;
③类比推理是由特殊到一般的推理;
④分析法是一种间接证明法;
⑤若z∈C,且|z+2﹣2i|=1,则|z﹣2﹣2i|的最小值是3.
A.①②③④ B.②③④ C.①②④⑤ D.①②⑤
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷(解析版) 题型:选择题
分析法是从要证的不等式出发,寻求使它成立的( )
A.充分条件 B.必要条件
C.充要条件 D.既不充分又不必要条件
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.2数学证明练习卷(解析版) 题型:选择题
(2014•泸州一模)一支人数是5的倍数且不少于1000人的游行队伍,若按每横排4人编队,最后差3人;若按每横排3人编队,最后差2人;若按每横排2人编队,最后差1人.则这只游行队伍的最少人数是( )
A.1025 B.1035 C.1045 D.1055
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.2数学证明练习卷(解析版) 题型:选择题
(2014•上海二模)一个机器人每一秒钟前进或后退一步,程序设计师让机器人以前进3步,然后再后退2步的规律移动.如果将机器人放在数轴的原点,面向正的方向,以1步的距离为1个单位长度.令P(n)表示第n秒时机器人所在位置的坐标,且记P(0)=0,则下列结论中错误的是( )
A.P(3)=3 B.P(5)=1 C.P(2003)>P(2005) D.P(2003)<P(2005)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 2.2结构图练习卷(解析版) 题型:选择题
某单位综合治理领导小组成员之问的领导关系可以用框图表示,这种框图通常称为( )
A.程序流程图 B.工序流程图 C.知识结构图 D.组织结构图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com