下列表述正确的是（ ）
①归纳推理是由特殊到一般的推理；
②演绎推理是由一般到特殊的推理；
③类比推理是由特殊到一般的推理；
④分析法是一种间接证明法；
⑤若z∈C，且|z+2﹣2i|=1，则|z﹣2﹣2i|的最小值是3．
A.①②③④ B.②③④ C.①②④⑤ D.①②⑤
D
【解析】
试题分析：本题考查的知识点是归纳推理、类比推理和演绎推理的定义，根据定义对①②③个命题逐一判断；分析法是一种直接证明法；考虑|Z+2﹣2i|=1的几何意义，表示以（﹣2，2）为圆心，以1为半径的圆，|Z﹣2﹣2i|的最小值，就是圆上的点到（2，2）距离的最小值，转化为圆心到（2，2）距离与半径的差，即可得到答案．
【解析】
归纳推理是由部分到整体、特殊到一般的推理，故①正确；
演绎推理是由一般到特殊的推理，故②正确；
类比推理是由特殊到特殊的推理，故③错误；
分析法是一种直接证明法，故④错误；
|z+2﹣2i|=1表示复平面上的点到（﹣2，2）的距离为1的圆，|z﹣2﹣2i|就是圆上的点，到（2，2）的距离的最小值，就是圆心到（2，2）的距离减去半径，即：|2﹣（﹣2）|﹣1=3，故⑤正确
故选：D．
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案科目：高中数学 来源：[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷（解析版） 题型：选择题
已知圆柱的底面半径为2，高为3，用一个与底面不平行的平面去截，若所截得的截面为椭圆，则椭圆的离心率的最大值为（ ）
A.1 B.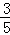
C.
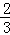D.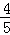
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷（解析版） 题型：填空题
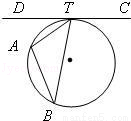
（2010•浙江模拟）如图，CD是⊙O的切线，T为切点，A是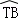 
上的一点，若∠TAB=100°，则∠BTD的度数为 ．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷（解析版） 题型：选择题
如图，PAB、PCD为⊙O的两条割线，AD、BC相交于点E，则图中相似三角形共有（ ）
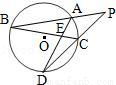
A.1对 B.2对 C.3对 D.4对
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷（解析版） 题型：选择题
下面对命题“函数f（x）=x+
是奇函数”的证明不是综合法的是（ ）
A.?x∈R且x≠0有f（﹣x）=（﹣x）+
=﹣（x+
）=﹣f（x），∴f（x）是奇函数
B.?x∈R且x≠0有f（x）+f（﹣x）=x++（﹣x）+（﹣）=0，∴f（x）=﹣f（﹣x），∴f（x）是奇函数
C.?x∈R且x≠0，∵f（x）≠0，∴
=
=﹣1，∴f（﹣x）=﹣f（x），∴f（x）是奇函数
D.取x=﹣1，f（﹣1）=﹣1+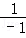
=﹣2，又f（1）=1+
=2
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷（解析版） 题型：选择题
命题“对于任意角θ，cos4θ﹣sin4θ=cos2θ”的证明：“cos4θ﹣sin4θ=（cos2θ﹣sin2θ）（cos2θ+sin2θ）=cos2θ﹣sin2θ=cos2θ”过程应用了（ ）
A.分析发
B.综合法
C.综合法、分析法结合使用
D.间接证法
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.2数学证明练习卷（解析版） 题型：选择题
（2014•郴州三模）设集合A⊆R，如果x0∈R满足：对任意a＞0，都存在x∈A，使得0＜|x﹣x0|＜a，那么称x0为集合A的一个聚点．则在下列集合中：
（1）Z+∪Z﹣；
（2）R+∪R﹣；
（3）{x|x=
，n∈N*}；
（4）{x|x=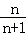
，n∈N*}．
其中以0为聚点的集合有（ ）
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.2数学证明练习卷（解析版） 题型：选择题
（2014•北京）加工爆米花时，爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”，在特定条件下，可食用率p与加工时间t（单位：分钟）满足函数关系p=at2+bt+c（a，b，c是常数），如图记录了三次实验的数据，根据上述函数模型和实验数据，可以得到最佳加工时间为（ ）
A.3.50分钟 B.3.75分钟 C.4.00分钟 D.4.25分钟
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
