
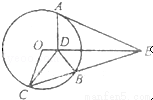
(2014•南开区二模)如图,AE是圆O的切线,A是切点,AD与OE垂直,垂足是D.割线EC交圆D于B,C,且∠BDC=62°,∠DBE=108°,则∠OEC= .
13
【解析】
试题分析:连接OA,OB,由已知条件得,△ADE∽△OAE,△BED∽△OEC,从而得O,C,B,D四点共圆,由此能求出结果.
【解析】
连接OA,OB,∵AE是⊙O切线∴∠OAE=90°
∵AD⊥OE,∴∠ADE=90°=∠OAE,又∵∠AED=∠OEA,
∴△ADE∽△OAE,∴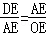 ,
,
∴AE2=DE×OE,∵AE2=BE×CE,∴DE×OE=BE×CE,
∴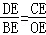 ,
,
又∵∠BED=∠OEC,∴△BED∽△OEC,
∴∠BDE=∠OCE,∴O,C,B,D四点共圆,
∵OB=OC,∴∠OBC=∠OCE,∴∠ODC=∠OBC,
∴∠ODC=∠BDE,∵∠BDC=62°
∴BDE=(180°﹣∠BDC)÷2=59°,
∴∠OEC=180°﹣∠DBE﹣∠BDE=13°.
故答案为:13.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
(2011•温州二模)将函数y=﹣sinx(x∈[0,π])的图象绕原点顺时针方向旋转角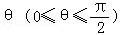 得到曲线C,对于每一个旋转角θ,曲线C都是一个函数的图象,则θ的最大值是( )
得到曲线C,对于每一个旋转角θ,曲线C都是一个函数的图象,则θ的最大值是( )
A. B.
B.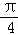 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷(解析版) 题型:选择题
已知圆柱的底面半径为2,高为3,用一个与底面不平行的平面去截,若所截得的截面为椭圆,则椭圆的离心率的最大值为( )
A.1 B.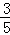 C.
C.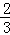 D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.1平行射影练习卷(解析版) 题型:选择题
(2005•静安区一模)Rt△ABC的直角边AB在平面α内,顶点C在平面α外,则直角边BC、斜边AC在平面α上的射影与直角边AB组成的图形是( )
A.线段或锐角三角形
B.线段与直角三角形
C.线段或钝角三角形
D.线段、锐角三角形、直角三角形或钝角三角形
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:填空题
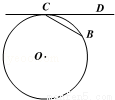
(2014•珠海二模)(几何证明选讲选做题)如图,CD是圆O的切线,切点为C,点B在圆O上,BC=2,∠BCD=30°,则圆O的面积为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:选择题
PT切⊙O于T,割线PAB经过O点交⊙O于A、B,若PT=4,PA=2,则cos∠BPT=( )
A.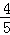 B.
B.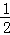 C.
C.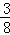 D.
D.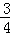
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷(解析版) 题型:填空题
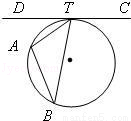
(2010•浙江模拟)如图,CD是⊙O的切线,T为切点,A是 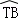 上的一点,若∠TAB=100°,则∠BTD的度数为 .
上的一点,若∠TAB=100°,则∠BTD的度数为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.2数学证明练习卷(解析版) 题型:选择题
(2014•郴州三模)设集合A⊆R,如果x0∈R满足:对任意a>0,都存在x∈A,使得0<|x﹣x0|<a,那么称x0为集合A的一个聚点.则在下列集合中:
(1)Z+∪Z﹣;
(2)R+∪R﹣;
(3){x|x= ,n∈N*};
,n∈N*};
(4){x|x=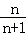 ,n∈N*}.
,n∈N*}.
其中以0为聚点的集合有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com