
分析 (1)解方程x3-3x=0便可得出y=f(x)的零点;
(2)根据增函数的定义,设任意的x1>x2≥1,然后作差,分解因式,提取公因式x1-x2,从而证明f(x1)>f(x2)便可得出f(x)在[1,+∞)上单调递增.
解答 解:(1)解x3-3x=0得,x=0,$-\sqrt{3}$,$\sqrt{3}$;
∴y=f(x)的零点为0,$-\sqrt{3}$,$\sqrt{3}$;
(2)证明:设x1>x2≥1,则:
$f({x}_{1})-f({x}_{2})={{x}_{1}}^{3}-3{x}_{1}-{{x}_{2}}^{3}+3{x}_{2}$=$({x}_{1}-{x}_{2})({{x}_{1}}^{2}+{x}_{1}{x}_{2}+{{x}_{2}}^{2}-3)$;
∵x1>x2≥1;
∴x1-x2>0,${{x}_{1}}^{2}>1,{x}_{1}{x}_{2}>1,{{x}_{2}}^{2}≥1$,${{x}_{1}}^{2}+{x}_{1}{x}_{2}+{{x}_{2}}^{2}-3>0$;
∴f(x1)>f(x2);
∴f(x)在[1,+∞)上是单调递增函数.
点评 考查函数零点的概念及求法,增函数的定义,以及根据增函数的定义证明一个函数为增函数的方法和过程,作差的方法比较f(x1),f(x2),作差后一般要提取公因式x1-x2,立方差公式的运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
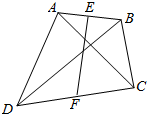 已知,如图所示,点E、F分别为任意四边形ABCD对边AB、CD的中点,求证:$\overrightarrow{EF}$=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{BD}$).
已知,如图所示,点E、F分别为任意四边形ABCD对边AB、CD的中点,求证:$\overrightarrow{EF}$=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{BD}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
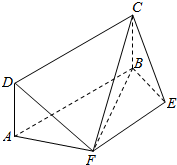 如图,矩形ABCD所在的平面与平面ABEF互相垂直,ABEF是等腰梯形,AB∥EF,AB=2,AD=AF=EF=BE=1.
如图,矩形ABCD所在的平面与平面ABEF互相垂直,ABEF是等腰梯形,AB∥EF,AB=2,AD=AF=EF=BE=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com