
【题目】如图,已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() 的中点.
的中点.
(Ⅰ)证明: ![]() ;
;
(Ⅱ)若![]() 为
为![]() 上的动点,
上的动点, ![]() 与平面
与平面![]() 所成最大角的正切值为
所成最大角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

【答案】(1)见解析(2)![]()
【解析】试题分析:(Ⅰ)由条件,可证菱形![]() 中,
中, ![]() ,再由线面垂直可得线线垂直得出
,再由线面垂直可得线线垂直得出![]() ,进一步得出
,进一步得出![]() 平面
平面![]() ,再由线面垂直的性质,可证线线垂直
,再由线面垂直的性质,可证线线垂直![]() (Ⅱ)由所给条件,建立以
(Ⅱ)由所给条件,建立以![]() 为坐标原点空间直角坐标系,写出空间各点坐标,求出二面角的二面的法向量,由法向量的夹角与二面角之间的关系求出其余弦值.
为坐标原点空间直角坐标系,写出空间各点坐标,求出二面角的二面的法向量,由法向量的夹角与二面角之间的关系求出其余弦值.
试题解析:(Ⅰ)证明:由四边形![]() 为菱形,
为菱形, ![]() ,可得
,可得![]() 为正三角形.
为正三角形.
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
又![]() ,因此
,因此![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .
.
而![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 且
且![]() ,
,
所以![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,所以
,所以![]() .
.
(Ⅱ)解:设![]() ,
, ![]() 为
为![]() 上任意一点,连接
上任意一点,连接![]() .
.
由(Ⅰ)知![]() 平面
平面![]() ,
, ![]() 为
为![]() 与平面
与平面![]() 所成的角.
所成的角.
在![]() 中,
中, ![]() ,所以当
,所以当![]() 最短时,
最短时, ![]() 最大,
最大,
即当![]() 时,
时, ![]() 最大.此时
最大.此时![]() ,
,
因此![]() .又
.又![]() ,所以
,所以![]() ,所以
,所以![]() .
.
方法1:因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .过
.过![]() 作
作![]() 于
于![]() ,由面面垂直的性质定理,
,由面面垂直的性质定理,
则![]() 平面
平面![]() ,过
,过![]() 作
作![]() 于
于![]() ,连
,连![]() ,则
,则![]() ,此时
,此时![]() 平面
平面![]() ,
,
显然![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,
, ![]() ,
,
在![]() 中,∵
中,∵![]() ,又
,又![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
因此在![]() 中,
中, ![]() ,又
,又![]() ,
,
在![]() 中,
中, 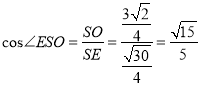 ,即所求二面角的余弦值为
,即所求二面角的余弦值为![]() .
.
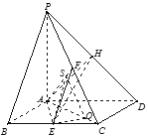
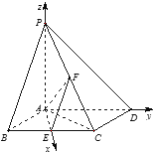
方法2:由(Ⅰ)知![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立如图所示的空间直角坐标系,
为坐标原点,建立如图所示的空间直角坐标系,
又![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ,
, 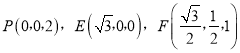 ,所以
,所以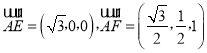 .
.
设平面![]() 的一法向量为
的一法向量为![]() ,则
,则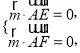 因此
因此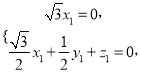
取![]() ,则
,则![]() ,因为
,因为![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,
,
故![]() 为平面
为平面![]() 的一法向量.又
的一法向量.又![]() ,所以
,所以 .因为二面角
.因为二面角![]() 为锐角,所以所求二面角的余弦值为
为锐角,所以所求二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某学校为加强学生的交通安全教育,对学校旁边![]() ,
,![]() 两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且
两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且![]() 路口数据的平均数比
路口数据的平均数比![]() 路口数据的平均数小2.
路口数据的平均数小2.
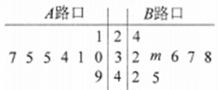
(1)求出![]() 路口8个数据中的中位数和茎叶图中
路口8个数据中的中位数和茎叶图中![]() 的值;
的值;
(2)在![]() 路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在互联网时代,网校培训已经成为青年学习的一种趋势,假设某网校的套题每日的销售量![]() (单位:千套)与销售价格
(单位:千套)与销售价格![]() (单位:元/套)满足的关系式
(单位:元/套)满足的关系式![]() (
(![]() ,
,![]() 为常数),其中
为常数),其中![]() 与
与![]() 成反比,
成反比,![]() 与
与![]() 的平方成正比,已知销售价格为5元/套时,每日可售出套题21千套,销售价格为3.5元/套时,每日可售出套题69千套.
的平方成正比,已知销售价格为5元/套时,每日可售出套题21千套,销售价格为3.5元/套时,每日可售出套题69千套.
(1) 求![]() 的表达式;
的表达式;
(2) 假设网校的员工工资,办公等所有开销折合为每套题3元(只考虑销售出的套数),试确定销售价格![]() 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
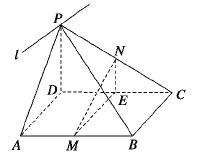
【题目】如图,P为平行四边形ABCD所在平面外一点,MN分别为ABPC的中点,平面PAD∩平面PBC=l.
(1)判断BC与l的位置关系,并证明你的结论;
(2)判断MN与平面PAD的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆x2+y2-6x-8y+21=0和直线kx-y-4k+3=0.
(1)若直线和圆总有两个不同的公共点,求k的取值集合
(2)求当k取何值时,直线被圆截得的弦最短,并求这最短弦的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(-2,0),N(2,0),动点P满足条件|PM|-|PN|=2![]() ,记动点P的轨迹为W.
,记动点P的轨迹为W.
⑴求W的方程;
⑵若A、B是W上的不同两点,O是坐标原点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列说法中正确的有( )
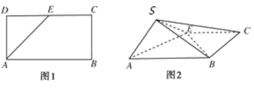
①存在点E使得直线SA⊥平面SBC;
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行;
④存在点E使得SE⊥BA.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业共有20条生产线,由于受生产能力和技术水平等因素的影响,会产生一定量的次品.根据经验知道,每台机器产生的次品数![]() 万件与每台机器的日产量
万件与每台机器的日产量![]() 万件
万件![]() 之间满足关系:
之间满足关系:![]() .已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
.已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
(Ⅰ)试将该企业每天生产这种产品所获得的利润![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)当每台机器的日产量为多少时,该企业的利润最大,最大为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com