练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，在直平行六面体ABCD-A1B1C1D1中，侧棱AA1=3，AB=3，BC=
    		3
    ，E为AB的中点且CE⊥A1E．
    （1）求证：平面A1EC⊥平面ABB1A1；
    （2）求二面角E-A1C-B1的大小．
    考点：二面角的平面角及求法,平面与平面垂直的判定
    专题：空间位置关系与距离,空间角
    分析：（1）由线面垂直，得AA1⊥EC，又A1E⊥EC，从而得到EC⊥面A1EC，由此能证明面A1EC⊥面ABB1A1．
    （2）过F作FG⊥A1C，连结B1G，由三垂线定理得B1G⊥A1C，∠B1GF为二面角E-A1C-B1的平面角，由此能求出二面角E-A1C-B1的大小．
    解答： 本题满分（12分）
    （1）证明：直平行六面体ABCD-A1B1C1D1中，
    AA1⊥面ABCD，EC?面ABCD，∴AA1⊥EC
    又A1E⊥EC，且AA1∩A1E=A，
    ∴EC⊥面A1EC，
    ∵EC?面A1EC，
    ∴面A1EC⊥面ABB1A1．…（4分）
    （2）解：过F作FG⊥A1C，连结B1G，
    由三垂线定理得B1G⊥A1C，
    ∴∠B1GF为二面角E-A1C-B1的平面角，
    在Rt△A1FB1中，A1B1=2，sin∠A1B1F=
    		10
    10
    ，
    ∴A1F=2•
    		10
    10
    =
    		10
    10
    ，
    又△A1FG：△A1EC，
    ∴
    FG
    A1F
    =
    EC
    A1C
    ⇒FG=A1F•
    EC
    A1C
    =
    		10
    5
    •
    		2
    2
    		3
    =
    		15
    15
    ，
    又在Rt△B1FG中，tan∠B1GF=
    B1F
    FG
    =
    3
    5
    		10
    		15
    15
    =3
    		6
    ，
    ∴二面角E-A1C-B1的大小为：arctan3
    		6
    ．…（12分）
    点评：本题考查面面垂直的证明，考查二面角大小的求法，解题时要认真审题，注意空间思维能力的培养．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    平面内有向量
    OA
    =（1，7），
    OB
    =（5，1），
    OP
    =（2，1），点M（x，y）为直线OP上的一动点．
    （1）用只含y的代数式表示
    OM
    的坐标；
    （2）求
    MA
    •
    MB
    的最小值，并写出此时
    OM
    的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某同学参加高二学业水平测试的4门必修科目考试．已知该同学每门学科考试成绩达到“A”等级的概率均为
    2
    3
    ，且每门考试成绩的结果互不影响．
    （1）求该同学至少得到两个“A”的概率；
    （2）已知在高考成绩计分时，每有一科达到“A”，则高考成绩加1分，如果4门学科均达到“A”，则高考成绩额外再加1分．现用随机变量Y表示该同学学业水平测试的总加分，求Y的概率分别列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

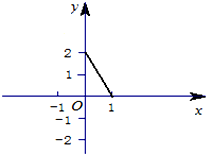    已知函数y=f（x）是定义在[-1，1]上的奇函数，当x∈（0，1]时的图象如图所示．
    （1）画出函数在[-1，0）上的图象；
    （2）求函数y=f（x）的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    阅读如图所示算法：
    （1）指出该算法表示的功能；
    （2）画出算法框图．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆C的极坐标方程为ρ2=
    12
    3cos2θ+4sin2θ
    ，点F1，F2为其左右焦点．以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
    x=2+
    		2
    2
    t
    y=
    		2
    2
    t
    （t为参数，t∈R）．
    （1）求直线l的普通方程和椭圆C的直角坐标方程；
    （2）求点F1，F2到直线l的距离之和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

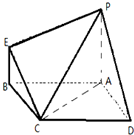    如图：ABCD是平行四边形，AP⊥平面ABCD，BE∥AP，AB=AP=2，BE=BC=1，∠CBA=60°
    （1）求证：EC∥平面PAD；
    （2）求证：平面PAC⊥平面EBC；
    （3）求直线PC与平面PABE所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，直角梯形PBCD，PD∥BC，∠D=90°，PD=9，BC=3，CD=4，点A在PD上，且PA=2AD，将△PAB沿AB折到△SAB的位置，使SB⊥BC．

    （Ⅰ）求证：SA⊥AD；
    （Ⅱ）点E在SD上，且
    SE
    =
    1
    3
    SD
    ，求二面角S-AC-E的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=|x-1|．
    （1）解关于x的不等式f（x）+x2-1＞0；
    （2）若f（x）＜-|x+3|+m的解集非空，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案