
(本小题满分12分)
如图,在□ABCD中,∠DAB=60°,AB=2,AD="4." 将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD. 
(1)求证:AB⊥DE;
(2)求三棱锥E—ABD的侧面积.
(1)先求出BD,利用勾股定理知AB⊥BD,再由面面垂直的性质知AB⊥平面EBD,从而得证(2)S=8+2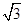
解析试题分析:(1)在△ABD 中,∵AB=2,AD=4,∠DAB=60°,
∴BD=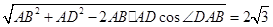 .
.
∴AB2+BD2=AD2,∴AB⊥BD.
又∵平面EBD⊥平面ABD,
平面EBD∩平面ABD=BD,AB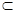 平面ABD,
平面ABD,
∴AB⊥平面EBD. 又∵DE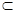 平面EBC,∴AB⊥DE. ……5分
平面EBC,∴AB⊥DE. ……5分
(2)由(1)知AB⊥BD.
∵CD∥AB ∴CD⊥BD,从而DE⊥BD
在Rt△DBE中, ∵DB=2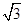 ,DE=DC=AB=2,
,DE=DC=AB=2,
∴S△DBE=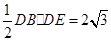 .……7分
.……7分
又∵AB⊥平面EBD,BE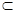 平面EBD,∴AB⊥BE.
平面EBD,∴AB⊥BE.
∵BE=BC=AD=4,S△ABE= AB·BE=4……9分
AB·BE=4……9分
∵DE⊥BD,平面EBD⊥平面ABD,∴ED⊥平面ABD,
而AD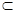 平面ABD,∴ED⊥AD,∴S△ADE=
平面ABD,∴ED⊥AD,∴S△ADE= AD·DE="4." ……11分
AD·DE="4." ……11分
综上,三棱锥E—ABD的侧面积S=8+2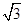 . ……12分
. ……12分
考点:本小题主要考查空间中直线、平面间的位置关系的判断和证明以及侧面积的计算,考查学生的空间想象能力和推理论证能力以及运算求解能力.
点评:要证明空间中直线、平面间的位置关系要紧扣判定定理和性质定理,定理中要求的条件缺一不可.


科目:高中数学 来源: 题型:解答题
(本小题满分10分)
如图所示是一个半圆柱 与三棱柱
与三棱柱 的组合体,其中,圆柱
的组合体,其中,圆柱 的轴截面
的轴截面 是边长为4的正方形,
是边长为4的正方形,
 为等腰直角三角形,
为等腰直角三角形, .
.
试在给出的坐标纸上画出此组合体的三视图.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,平面 ⊥平面
⊥平面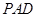 ,
, 是直角三角形,
是直角三角形,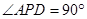 ,四边形
,四边形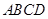 是直角梯形,其中
是直角梯形,其中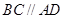 ,
,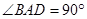 ,
, ,且
,且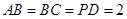 ,
,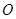 是
是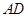 的中点,
的中点,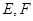 分别是
分别是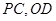 的中点.
的中点. 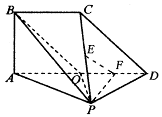
(Ⅰ)求证: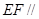 平面
平面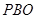 ;
;
(Ⅱ)求二面角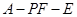 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)如图所示,直三棱柱ABC—A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求 的长; (2)求cos<
的长; (2)求cos< >的值; (3)求证:A1B⊥C1M.
>的值; (3)求证:A1B⊥C1M.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知梯形ABCD中,AD∥BC,∠ABC ="∠BAD" = ,AB=BC=2AD=4,E、F分别是AB、CD上的点,且EF∥BC。设AE =
,AB=BC=2AD=4,E、F分别是AB、CD上的点,且EF∥BC。设AE = ,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
(1)当 =2时,求证:BD⊥EG ;
=2时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为 ,求
,求 的最大值;
的最大值;
(3)当 取得最大值时,求二面角D-BF-E的余弦值.
取得最大值时,求二面角D-BF-E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.
(1)求证:平面 平面
平面 ;
;
(2)在底面A1D1上有一个靠近D1的四等分点H,求证: EH∥平面FGB1;
(3)求四面体EFGB1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
如图,在直三棱柱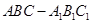 (侧棱垂直于底面的棱柱)中,
(侧棱垂直于底面的棱柱)中,  ,
, 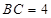 ,
, 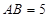 ,
,  ,点
,点 是
是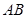 的中点.
的中点. 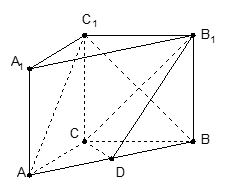
(Ⅰ) 求证: ∥平面
∥平面 ;
;
(Ⅱ)求AC1与平面CC1B1B所成的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com