
【题目】已知函数![]() .
.
(1)求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(2)在曲线![]() 上是否存在点P,使得过点P可作三条直线与曲线
上是否存在点P,使得过点P可作三条直线与曲线![]() 相切?若存在,求出其横坐标的取值范围;若不存在,请说明理由.
相切?若存在,求出其横坐标的取值范围;若不存在,请说明理由.
【答案】(1)当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,![]() ;(2)存在,
;(2)存在, .
.
【解析】
(1)求出导数![]() ,确定函数的单调性,然后按
,确定函数的单调性,然后按![]() 分类讨论;
分类讨论;
(2)假设存在符合条件的点![]() ,同时设切点为
,同时设切点为![]() ,由导数几何意义得
,由导数几何意义得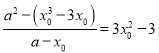 即
即![]() (*),问题转化为关于
(*),问题转化为关于![]() 的方程(*)存在三个不同实根.然后用导数研究函数
的方程(*)存在三个不同实根.然后用导数研究函数![]() 的零点.
的零点.
(1)由题意得:![]()
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
即![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
又![]() 的零点分别为
的零点分别为![]() ,0,
,0,![]()
所以当![]() 时,
时,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() .
.
(2)假设存在符合条件的点![]() ,切点设为
,切点设为![]()
所以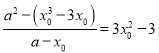 即
即![]() (*)
(*)
故问题转化为关于![]() 的方程(*)存在三个不同实根.
的方程(*)存在三个不同实根.
令![]() ,则
,则![]()
当![]() 时,
时,![]() ,
,![]() 在R上单调递增,不合题意;
在R上单调递增,不合题意;
当![]() 时,易知
时,易知![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
从而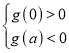 ,即
,即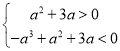
解得:![]()
当![]() 时,易知
时,易知![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
从而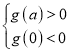 ,即
,即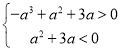
解得:![]()
综上,存在符合条件的点P,其横坐标的取值范围为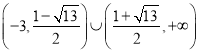 .
.


科目:高中数学 来源: 题型:
【题目】如图所示,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,AB=1,BC=![]() ,AA1=2,E是侧棱BB1的中点.
,AA1=2,E是侧棱BB1的中点.
(1)求证:A1E⊥平面AED;
(2)求二面角A﹣A1D﹣E的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是关于的方程组
是关于的方程组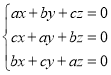 的解.
的解.
(1)求证: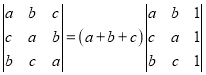 ;
;
(2)设![]() 分别为
分别为![]() 三边长,试判断
三边长,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)设![]() 为不全相等的实数,试判断
为不全相等的实数,试判断![]() 是“
是“![]() ”的 条件,并证明.①充分非必要;②必要非充分;③充分且必要;④非充分非必要.
”的 条件,并证明.①充分非必要;②必要非充分;③充分且必要;④非充分非必要.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节是中国传统节日之一节日期间,各大商场各种品牌的“粽子战”便悄然打响.某记者走访市场发现,各大商场粽子种类繁多,价格不一根据数据统计分析,得到了某商场不同种类的粽子销售价格(单位:元/千克)的频数分布表,如表一所示.
表一:
价格/(元/千克) | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) |
种类数 | 4 | 12 | 16 | 6 | 2 |
在调查中,记者还发现,各大品牌在馅料方面还做足了功课,满足了市民多样化的需求除了蜜枣、豆沙等传统馅料粽,很多品牌还推出了鲜肉、巧克力、海鲜等特色馅料粽在该商场内,记者随机对100名顾客的年龄和粽子口味偏好进行了调查,结果如表二.
表二:
喜欢传统馅料粽 | 喜欢特色馅料粽 | 总计 | |
40岁以下 | 30 | 15 | 45 |
40岁及以上 | 50 | 5 | 55 |
总计 | 80 | 20 | 100 |
(1)根据表一估计该商场粽子的平均销售价(同一组中的数据用该组区间的中点值代表);
(2)根据表二信息能否有95%的把握认为顾客的粽子口味偏好与年龄有关?
参考公式和数据: (其中
(其中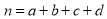 为样本容量)
为样本容量)
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某制药厂准备投入适当的广告费,对产品进行宣传,在一年内,预计年销量Q(万件)与广告费x(万元)之间的函数关系为Q![]() (x≥0).已知生产此产品的年固定投入为3万元,每生产1万件此产品仍需后期再投入32万元,若每件售价为“年平均每件投入的150%”与“年平均每件所占广告费的50%”之和(注:投入包括“年固定投入”与“后期再投入”).
(x≥0).已知生产此产品的年固定投入为3万元,每生产1万件此产品仍需后期再投入32万元,若每件售价为“年平均每件投入的150%”与“年平均每件所占广告费的50%”之和(注:投入包括“年固定投入”与“后期再投入”).
(1)试将年利润w万元表示为年广告费x万元的函数,并判断当年广告费投入100万元时,企业亏损还是盈利?
(2)当年广告费投入多少万元时,企业年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且椭圆
,且椭圆![]() 的一个顶点
的一个顶点![]() 的坐标为
的坐标为![]() .过椭圆
.过椭圆![]() 的右焦点
的右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() (
(![]() ,
,![]() 不同于点
不同于点![]() ),直线
),直线![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() .连接
.连接![]() ,过点
,过点![]() 作
作![]() 的垂线与直线
的垂线与直线![]() 交于点
交于点![]() .
.
(1)求椭圆![]() 的方程,并求点
的方程,并求点![]() 的坐标;
的坐标;
(2)求证:![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),边长为![]() 的正方形
的正方形![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() ,现沿
,现沿![]() 把
把![]() 剪切、拼接成如图(2)的图形,再将
剪切、拼接成如图(2)的图形,再将![]() ,
,![]() ,
,![]() 沿
沿![]() ,
,![]() ,
,![]() 折起,使
折起,使![]() 、
、![]() 、
、![]() 三点重合于点
三点重合于点![]() ,如图(3).
,如图(3).
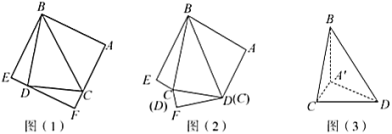
(1)求证:![]() ;
;
(2)求二面角![]() 最小时的余弦值.
最小时的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在开展创建“全国文明城市”活动中,工作有序扎实,成效显著,尤其是城市环境卫生大为改观,深得市民好评.“创文”过程中,某网站推出了关于环境治理和保护问题情况的问卷调查,现从参与问卷调查的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
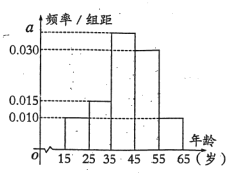
(1)求出a的值;
(2)若已从年龄较小的第1,2组中用分层抽样的方法抽取5人,现要再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为![]() ,墙
,墙![]() 的长度为
的长度为![]() 米,(已有两面墙的可利用长度足够大),记
米,(已有两面墙的可利用长度足够大),记![]() .
.
(1)若![]() ,求
,求![]() 的周长(结果精确到0.01米);
的周长(结果精确到0.01米);
(2)为了使小动物能健康成长,要求所建的三角形露天活动室面积,![]() 的面积尽可能大,当
的面积尽可能大,当![]() 为何值时,该活动室面积最大?并求出最大面积.
为何值时,该活动室面积最大?并求出最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com