
【题目】已知![]() 是关于的方程组
是关于的方程组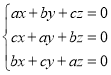 的解.
的解.
(1)求证: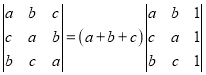 ;
;
(2)设![]() 分别为
分别为![]() 三边长,试判断
三边长,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)设![]() 为不全相等的实数,试判断
为不全相等的实数,试判断![]() 是“
是“![]() ”的 条件,并证明.①充分非必要;②必要非充分;③充分且必要;④非充分非必要.
”的 条件,并证明.①充分非必要;②必要非充分;③充分且必要;④非充分非必要.
【答案】(1)见解析(2)等边,见解析(3)④,见解析
【解析】
(1)将行列式的前两列加到第三列上即可得出结论;
(2)由方程组有非零解得出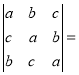 0,即
0,即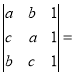 0,将行列式展开化简即可得出a=b=c;
0,将行列式展开化简即可得出a=b=c;
(3)利用(1),(2)的结论即可答案.
(1)证明:将行列式的前两列加到第三列上,
得: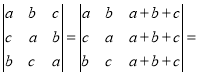 (a+b+c)
(a+b+c) .
.
(2)∵z0=1,∴方程组有非零解,
∴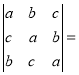 0,由(1)可知(a+b+c)
0,由(1)可知(a+b+c)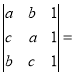 0.
0.
∵a、b、c分别为△ABC三边长,∴a+b+c≠0,
∴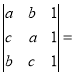 0,即a2+b2+c2﹣ab﹣bc﹣ac=0,
0,即a2+b2+c2﹣ab﹣bc﹣ac=0,
∴2a2+2b2+2c2﹣2ab﹣2bc﹣2ac=0,即(a﹣b)2+(b﹣c)2+(a﹣c)2=0,
∴a=b=c,
∴△ABC是等边三角形.
(3)若a+b+c=0,显然(0,0,0)是方程组的一组解,即x02+y02+z02=0,
∴a+b+c=0”不是“x02+y02+z02>0”的充分条件;
若x02+y02+z02>0,则方程组有非零解,
∴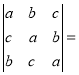 (a+b+c)
(a+b+c)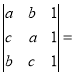 0.
0.
∴a+b+c=0或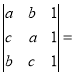 0.
0.
由(2)可知a+b+c=0或a=b=c.
∴a+b+c=0”不是“x02+y02+z02>0”的必要条件.
故答案为④.


科目:高中数学 来源: 题型:
【题目】设抛物线C:![]() 与直线
与直线![]() 交于A、B两点.
交于A、B两点.
(1)当![]() 取得最小值为
取得最小值为![]() 时,求
时,求![]() 的值.
的值.
(2)在(1)的条件下,过点![]() 作两条直线PM、PN分别交抛物线C于M、N(M、N不同于点P)两点,且
作两条直线PM、PN分别交抛物线C于M、N(M、N不同于点P)两点,且![]() 的平分线与
的平分线与![]() 轴平行,求证:直线MN的斜率为定值.
轴平行,求证:直线MN的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球教练对甲乙两位运动员在近五场比赛中的得分情况统计如下图所示,根据图表给出如下结论:(1)甲乙两人得分的平均数相等且甲的方差比乙的方差小;(2)甲乙两人得分的平均数相等且甲的方差比乙的方差大;(3)甲的成绩在不断提高,而乙的成绩无明显提高;(4)甲的成绩较稳定,乙的成续基本呈上升状态;结论正确的是( )
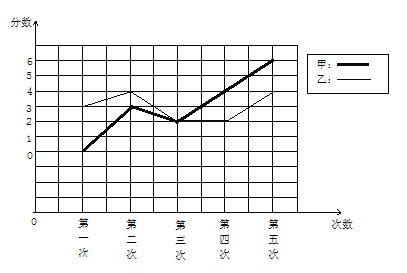
A.(1)(3)B.(1)(4)C.(2)(3)D.(2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)过椭圆 上异于其顶点的任意一点Q作圆
上异于其顶点的任意一点Q作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在x轴,y轴上的截距分别为
在x轴,y轴上的截距分别为![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)若![]() 是椭圆
是椭圆![]() 上不同两点,
上不同两点,![]() 轴,圆E过
轴,圆E过![]() ,且椭圆
,且椭圆![]() 上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆
上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆![]() 是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于任意![]() ,满足条件
,满足条件![]() 且
且![]() (M是与n无关的常数)的无穷数列
(M是与n无关的常数)的无穷数列![]() 称为M数列.
称为M数列.
(1)若等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,判断数列
,判断数列![]() 是否是M数列,并说明理由;
是否是M数列,并说明理由;
(2)若各项为正数的等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,证明:数列
,证明:数列![]() 是M数列,并指出M的取值范围;
是M数列,并指出M的取值范围;
(3)设数列![]() ,问数列
,问数列![]() 是否是M数列?请说明理由.
是否是M数列?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(2)在曲线![]() 上是否存在点P,使得过点P可作三条直线与曲线
上是否存在点P,使得过点P可作三条直线与曲线![]() 相切?若存在,求出其横坐标的取值范围;若不存在,请说明理由.
相切?若存在,求出其横坐标的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商贸公司售卖某种水果.经市场调研可知:在未来![]() 天内,这种水果每箱的销售利润
天内,这种水果每箱的销售利润![]() (单位:元)与时间
(单位:元)与时间![]() ,单位:天)之间的函数关系式为
,单位:天)之间的函数关系式为![]() , 且日销售量
, 且日销售量![]() (单位:箱)与时间
(单位:箱)与时间![]() 之间的函数关系式为
之间的函数关系式为![]()
①第![]() 天的销售利润为__________元;
天的销售利润为__________元;
②在未来的这![]() 天中,公司决定每销售
天中,公司决定每销售![]() 箱该水果就捐赠
箱该水果就捐赠![]() 元给 “精准扶贫”对象.为保证销售积极性,要求捐赠之后每天的利润随时间
元给 “精准扶贫”对象.为保证销售积极性,要求捐赠之后每天的利润随时间![]() 的增大而增大,则
的增大而增大,则![]() 的最小值是__________.
的最小值是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com