
【题目】正三角形![]() 的边长为2,将它沿高
的边长为2,将它沿高![]() 翻折,使点
翻折,使点![]() 与点
与点![]() 间的距离为
间的距离为![]() ,此时四面体
,此时四面体![]() 外接球表面积为__________.
外接球表面积为__________.
【答案】![]()
【解析】分析:由题意将几何体补形为三棱柱,结合三棱柱的几何特征整理计算即可求得最终结果.
详解:根据题意可知三棱锥BACD的三条侧棱BD⊥AD、DC⊥DA,
底面是等腰三角形,它的外接球就是它扩展为三棱柱的外接球,
求出三棱柱的底面中心连线的中点到顶点的距离,就是球的半径,
三棱柱的底面边长为1,1,![]() ,
,
由题意可得:三棱柱上下底面中点连线的中点,到三棱柱顶点的距离相等,说明中心就是外接球的球心,
∴三棱柱的外接球的球心为O,外接球的半径为r,
棱柱的高为![]() ,球心到底面的距离为
,球心到底面的距离为![]() ,
,
三棱柱中,底面△BDC,BD=CD=1,BC=![]() ,∴∠BDC=120°,
,∴∠BDC=120°,
△BDC的外接圆的半径为:![]() ,
,
∴球的半径为![]() .
.
外接球的表面积为:![]() .
.
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为日.(结果保留一位小数,参考数据:lg2≈0.30,lg3≈0.48)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆 ![]() :
: ![]() (其中
(其中 ![]() 为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线
为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线 ![]() .
.
(1)求曲线 ![]() 的方程;
的方程;
(2)若点 ![]() 为曲线
为曲线 ![]() 上一点,过点
上一点,过点 ![]() 作曲线
作曲线 ![]() 的切线交圆
的切线交圆 ![]() 于不同的两点
于不同的两点 ![]() (其中
(其中 ![]() 在
在 ![]() 的右侧),已知点
的右侧),已知点 ![]() .求四边形
.求四边形 ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种产品,每生产1吨产品需人工费4万元,每天还需固定成本3万元.经过长期调查统计,每日的销售额![]() (单位:万元)与日产量
(单位:万元)与日产量![]() (单位:吨)满足函数关系
(单位:吨)满足函数关系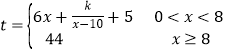 ,已知每天生产4吨时利润为7万元.
,已知每天生产4吨时利润为7万元.
(1)求![]() 的值;
的值;
(2)当日产量为多少吨时,每天的利润最大,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.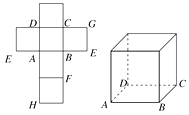
(1)请按字母F、G、H标记在正方体相应地顶点处(不需要说明理由);
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论;
(3)证明:直线DF⊥平面BEG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为
的右焦点为 ![]() ,上顶点为
,上顶点为 ![]() ,
, ![]() 周长为
周长为 ![]() ,离心率为
,离心率为 ![]() .
.
(1)求椭圆 ![]() 的方程;
的方程;
(2)若点 ![]() 是椭圆
是椭圆 ![]() 上第一象限内的一个点,直线
上第一象限内的一个点,直线 ![]() 过点
过点 ![]() 且与直线
且与直线 ![]() 平行,直线
平行,直线 ![]() 且
且 ![]() 与椭圆
与椭圆 ![]() 交于
交于 ![]() 两点,与
两点,与 ![]() 交于点
交于点 ![]() ,是否存在常数
,是否存在常数 ![]() ,使
,使 ![]() .若存在,求出
.若存在,求出 ![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com