
分析 (1)利用二倍角公式及变形,两角差的正弦公式化简解析式,由三角函数的周期公式、正弦函数的对称轴分别列出方程,求出ω的值可得f(x)的解析式;
(2)由(1)化简g(x),由x的范围2x-$\frac{π}{6}$的范围,由正弦函数的图象与性质求出$sin(2x-\frac{π}{6})$的范围,将
g(x)的零点问题转化为两个函数图象的交点问题,由条件和正弦函数的图象列出不等式,求出实数a的取值范围;
(3)由(2)和正弦函数的对称性证明出结论.
解答 解:(1)由题意得,f(x)=$\sqrt{3}$sinωxcosωx-cos2ωx+$\frac{3}{2}$
=$\frac{\sqrt{3}}{2}sin2ωx-\frac{1}{2}(1+cos2ωx)+\frac{3}{2}$=$sin(2ωx-\frac{π}{6})+1$,
∵f(x)的最小正周期为π,∴$\frac{2π}{2|ω|}=π$,则ω=±1,
∵图象关于直线x=$\frac{π}{6}$对称,
∴$2ω×\frac{π}{6}-\frac{π}{6}=\frac{π}{2}+kπ(k∈Z)$,得ω=2+3k(k∈Z),即ω=-1,
∴f(x)=$sin(-2x-\frac{π}{6})+1$=$-sin(2x+\frac{π}{6})+1$;
(2)由(1)得,g(x)=f(-x)+a=$sin(2x-\frac{π}{6})+1+a$,
∵0$≤x≤\frac{π}{2}$,∴$-\frac{π}{6}≤2x-\frac{π}{6}≤\frac{5π}{6}$,则$-\frac{1}{2}≤sin(2x-\frac{π}{6})≤1$,
∵函数g(x)=f(-x)+a(0$≤x≤\frac{π}{2}$)有且只有一个零点,
∴y=$sin(2x-\frac{π}{6})$和y=-1-a的图象有且仅有一个交点,
∴$-\frac{1}{2}≤-1-a<\frac{1}{2}$或-1-a=1,
解得$-\frac{3}{2}<a≤-\frac{1}{2}$或a=-2,
∴实数a的取值范围是{a|a=-2或$-\frac{3}{2}<a≤-\frac{1}{2}$};
证明:(3)∵x1,x2是函数g(x)的两个不同零点,
∴由(2)得,$2{x}_{1}-\frac{π}{6}$与$2{x}_{2}-\frac{π}{6}$关于直线x=$\frac{π}{2}$对称,
∴$2{x}_{1}-\frac{π}{6}$+($2{x}_{2}-\frac{π}{6}$)=$2×\frac{π}{2}$,
化简得x1+x2=$\frac{2π}{3}$.
点评 本题考查了二倍角公式及变形、两角差的正弦公式,正弦函数的图象与性质的应用,以及函数零点的转化,考查整体思想,转化思想,化简、变形能力.


科目:高中数学 来源: 题型:解答题
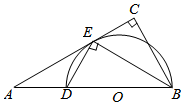 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB,且AD=2$\sqrt{3}$,AE=6
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB,且AD=2$\sqrt{3}$,AE=6查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\frac{{\sqrt{2e}}}{2e}+1)$ | B. | $(0,\frac{{\sqrt{2e}}}{2e})$ | C. | $(1,\frac{1}{e}+1)$ | D. | $(\frac{{\sqrt{2e}}}{2e},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com