
分析 (1)由两角和的正弦公式化简解析式,由正弦函数的值域求出f(x)的值域,由条件列出不等式,求出m的取值范围;
(2)根据正弦函数的增区间和整体思想求出函数f(x)的单调增区间.
解答 解:(1)由题意得,
f(x)=$\sqrt{3}$sinπx+cosπx=$2sin(πx+\frac{π}{6})$,
∴f(x)的值域是[-2,2],
∵方程f(x)=2m-3有实数解,
∴-2≤2m-3≤2,解得;$\frac{1}{2}≤m≤\frac{5}{2}$,
∴m的取值范围是[$\frac{1}{2}$,$\frac{5}{2}$];
(2)由$-\frac{π}{2}+2kπ≤πx+\frac{π}{6}≤\frac{π}{2}+2kπ(k∈Z)$得,
$-\frac{2}{3}+2k≤x≤\frac{1}{3}+2k(k∈Z)$,
∴f(x)单调递增区间是$[-\frac{2}{3}+2k,\frac{1}{3}+2k](k∈Z)$.
点评 本题考查了两角和的正弦公式,以及正弦函数的图象与性质,考查整体思想,化简、变形能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
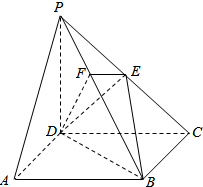 在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且PD=CD=$\frac{\sqrt{2}}{2}$BC,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.
在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且PD=CD=$\frac{\sqrt{2}}{2}$BC,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD是正方形.侧棱PA⊥底面ABCD.M、N分别为PD、AC的中点.
在四棱锥P-ABCD中,底面ABCD是正方形.侧棱PA⊥底面ABCD.M、N分别为PD、AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-1,1) | C. | (-∞,1) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com