
分析 (1)根据分式函数的性质,利用分子常数化进行求解.
(2)分母进行平方,利用一元二次函数以及分式函数的性质进行求解,
(3)利用换元法转化为一元二次函数进行求解.
(4)利用分式的性质,结合基本不等式的应用进行求解.
解答 解:(1)y=$\frac{3x+1}{x-2}$=$\frac{3(x-2)+7}{x-2}$=3+$\frac{7}{x-2}$,则y≠3,
即函数的值域为(-∞,3)∪(3,+∞);
(2)y=$\frac{5}{2{x}^{2}-4x+3}$=$\frac{5}{2(x-1)^{2}+1}$,
∵2(x-1)2+1≥1,∴$\frac{5}{2(x-1)^{2}+1}$∈(0,5],即函数的值域为(0,5];
(3)由1-x≥0得x≤1,则函数的定义域为(-∞,1],
设t=$\sqrt{1-x}$,则x=1-t2,t≥0,
则y=x+4$\sqrt{1-x}$=1-t2+4t=-(t-2)2+5,
∵t≥0,∴y≤5,即函数的值域为(-∞,5]
(4)y=$\frac{{x}^{2}}{x-1}$=$\frac{(x-1)^{2}+2(x-1)+1}{x-1}$=x-1+$\frac{1}{x-1}$+2,
∵x>1,∴x-1>0,
则y=x-1+$\frac{1}{x-1}$+2≥2+2$\sqrt{(x-1)•\frac{1}{x-1}}$=2+2=4,
当且仅当x-1=$\frac{1}{x-1}$,解集x-1=1,x=2时,取等号,
故函数的值域为[4,+∞).
点评 本题主要考查函数值域的求解,涉及几种常见求函数值域的方法.要求根据不同的条件选择合适的方法.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:解答题
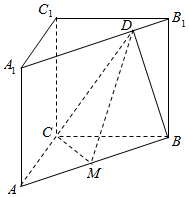 如图,直角三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1,M为AB的中点,D在A1B1上且A1D=3DB1.
如图,直角三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1,M为AB的中点,D在A1B1上且A1D=3DB1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为直角梯形,∠ABC=90°,AD∥BC,∠BCD=45°,AB=AD=PB=1,点E在棱PA上,且PE=2EA.
如图,四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为直角梯形,∠ABC=90°,AD∥BC,∠BCD=45°,AB=AD=PB=1,点E在棱PA上,且PE=2EA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com