
分析 (Ⅰ)求出函数的导数,计算f′(1),f(1),求出切线方程即可;
(Ⅱ)求出f(x)的导数,得到f(x)递增,从而证出结论即可.
解答 解:(Ⅰ)f(x)=ex-$\frac{{{{(x+1)}^2}}}{2}$,f(1)=e-2,
f′(x)=ex-(x+1),f′(1)=e-2,
∴切线方程是:y-e+2=(e-2)(x-1),
即y=(e-2)x;
(Ⅱ)f′(x)=ex-(x+1),f″(x)=ex-1,(x>-1),
令f″(x)>0,解得:x>0,令f″(x)<0,解得:-1<x<0,
∴f′(x)在(-1,0)递减,在(0,+∞)递增,
∴f′(x)>f′(0)=0,
∴f(x)在(-1,+∞)递增,
∴f(x)>f(-1)=$\frac{1}{e}$>0.
点评 本题考查了曲线的切线方程问题,考查函数的单调性问题,考查导数的应用,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
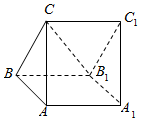 如图,三棱柱ABC-A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<m<$\frac{1}{3}$ | B. | 0<m≤$\frac{1}{3}$ | C. | $\frac{1}{3}$<m<1 | D. | $\frac{1}{3}$<m≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{8}$,+∞) | B. | ($\frac{1}{3}$,$\frac{{2\sqrt{2}}}{3}$) | C. | ($\frac{{\sqrt{2}}}{4}$,+∞) | D. | (2$\sqrt{2}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
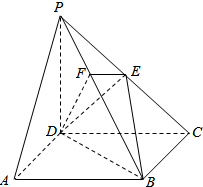 在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且PD=CD=$\frac{\sqrt{2}}{2}$BC,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.
在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且PD=CD=$\frac{\sqrt{2}}{2}$BC,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com