
分析 (Ⅰ)由二倍角公式和辅助角公式化简解析式,由此得到最小正周期.
(Ⅱ)由x的范围得到2x-$\frac{π}{3}$的范围,由此得到f(x)的值域.
解答 解:(Ⅰ)∵f(x)=sinxcosx-$\sqrt{3}{cos^2}$x,
=$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x-$\frac{\sqrt{3}}{2}$,
=sin(2x-$\frac{π}{3}$)-$\frac{\sqrt{3}}{2}$,
∴f(x)的最小正周期为T=π.
(Ⅱ)∵x∈[0,$\frac{π}{2}$],
∴2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],
∴sin(2x-$\frac{π}{3}$)-$\frac{\sqrt{3}}{2}$∈[-$\sqrt{3}$,1-$\frac{\sqrt{3}}{2}$]
∴f(x)的最大值和最小值分别为1-$\frac{\sqrt{3}}{2}$和-$\sqrt{3}$.
点评 本题考查解析式的化简和由x的范围得到f(x)的值域问题,需熟练掌握公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
 执行如图所示的程序框图,已知命题p:?k∈[4,6],输出S的值为30;命题q:?k∈(4,5),输出S的值为14,则下列命题正确的是( )
执行如图所示的程序框图,已知命题p:?k∈[4,6],输出S的值为30;命题q:?k∈(4,5),输出S的值为14,则下列命题正确的是( )| A. | q | B. | p∧q | C. | (¬p)∨q | D. | p(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\frac{9}{2}$ | C. | $\frac{5}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{8}$ | B. | $\frac{3π}{4}$ | C. | $\frac{3π}{2}$ | D. | 3π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在区间(0,$\frac{π}{6}$)上单调递增 | |
| B. | f(x)的一个对称中心为(-$\frac{π}{12}$,0) | |
| C. | 当x∈[0,$\frac{π}{3}$]时,fx)的值域为[1,$\sqrt{3}$] | |
| D. | 先将函数f(x)的图象的纵坐标不变,横坐标缩短为原来的$\frac{1}{2}$倍,再向左平移$\frac{π}{8}$个单位后得到函数y=2cos(4x+$\frac{π}{6}$)的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
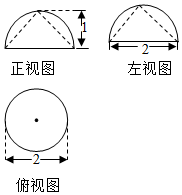
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2}{3}π$ | D. | $({2-\sqrt{2}})π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com